What is the equation of the parabola that has a vertex at # (-18, -12) # and passes through point # (-3,7) #?
2 Answers
Explanation:
Use the general quadratic formula,
Since the vertex is given
The only unkown variable left is
Finally, the equation of the quadratic is,
graph{19/225(x+18)^2-12 [-58.5, 58.53, -29.26, 29.25]}
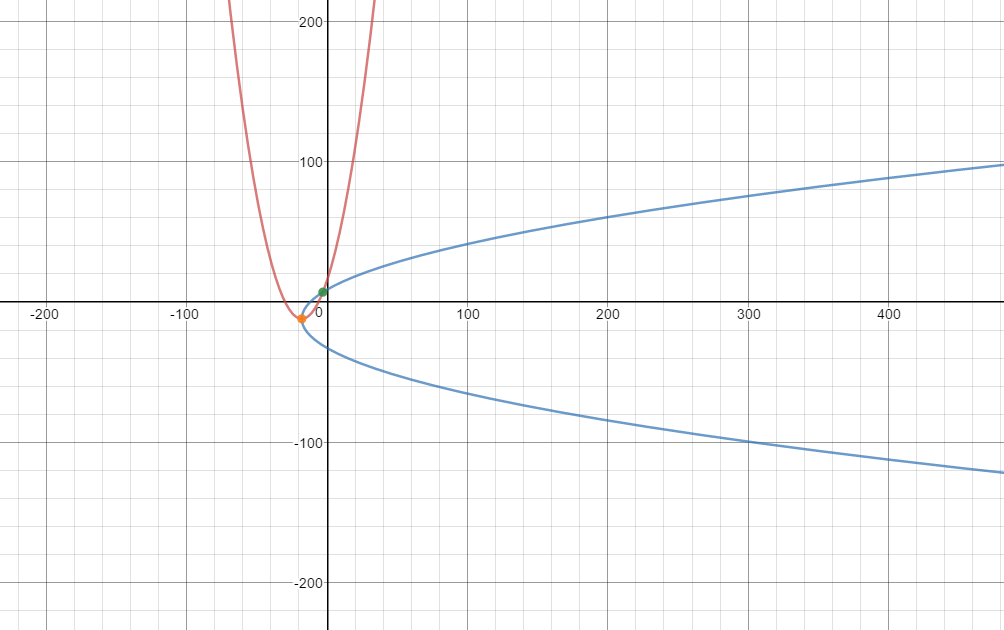
There are two equations that represent two parabolas that have the same vertex and pass through the same point. The two equations are:
Explanation:
Using the vertex forms:
Substitute
Substitute
Solve for both values of
The two equations are:
Here is a graph of the two points and the two parabolas: