Question

What is the equation of the parabola that has a vertex at `(38, -22)` and passes through point `(3,7)`?

Answer 1

There are 2 standard equations:

`y = 29/1225(x-38)^2-22`

`x = -35/841(y-(-22))^2+38`

Explanation:

Actually, there are two such parabolas, one whose general vertex form is:

`y = a(x-h)^2+k" [1]"`

and the other whose general vertex form is:

`x = a(y-k)^2+h" [2]"`

where `(h,k)` is the vertex and "a" is found by substituting in the given point `(x,y)`

Substitute the vertex `(38,-22)` into equations [1] and [2]:

`y = a(x-38)^2-22" [1.1]"`

`x = a(y-(-22))^2+38" [2.1]"`

Substitute the point `(3,7)` into equations [1.2] and [2.1] and then solve for "a":

`7 = a(3-38)^2-22` and `3 = a(7-(-22))^2+38`

`29 = a(3-38)^2` and `-35 = a(7-(-22))^2`

`29 = a(-35)^2` and `-35 = a(29)^2`

`a = 29/1225` and `a = -35/841`

Substitute the values for "a" into its respective equation:

`y = 29/1225(x-38)^2-22" [1.2]"`

`x = -35/841(y-(-22))^2+38" [2.2]"`

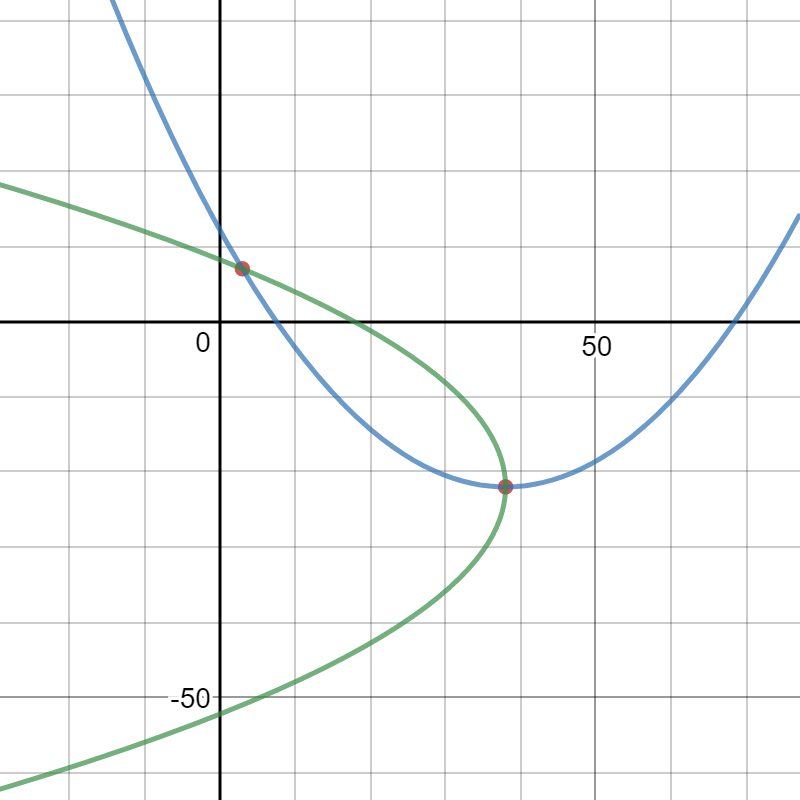
Here is a graph of the two points and both parabolas: