What is the equation of the tangent line of #f(x) = e^(x)/(x^2-x# at #x=3#?
1 Answer
May 27, 2018
Explanation:
For the equation of the tangent line at
The equation will be
and a graph
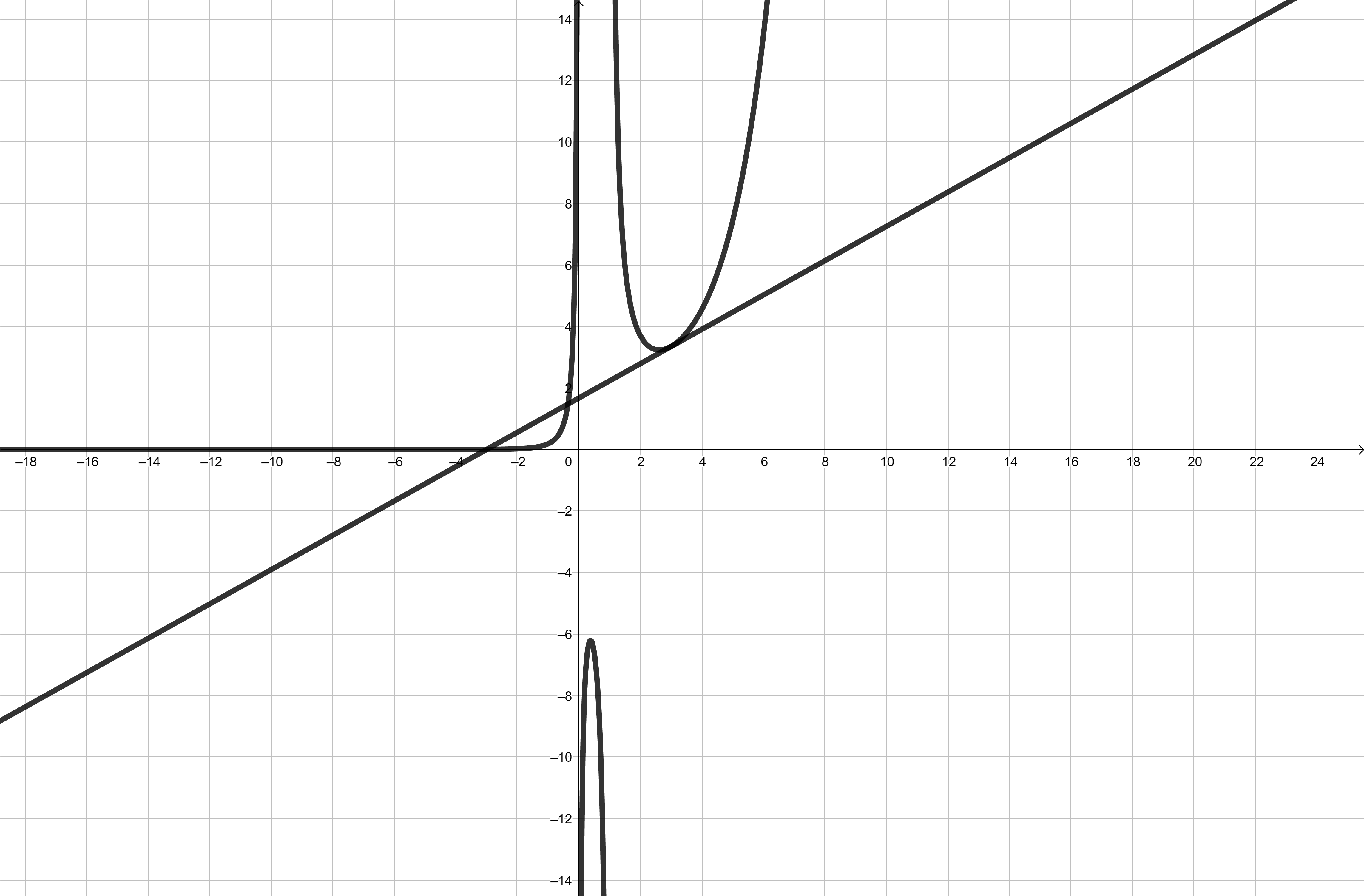
For the equation of the tangent line at
The equation will be
and a graph
