What is the equation of the tangent line of #f(x) = sec^3x^2# at #x=pi/8#?
1 Answer
Explanation:
At
And the slope is given by
# = 6xsec^3(x^2)tan(x^2)#
At
# = (3pi)/4sec^3(pi^2/64)tan(pi^2/64)#
the equation of the line through
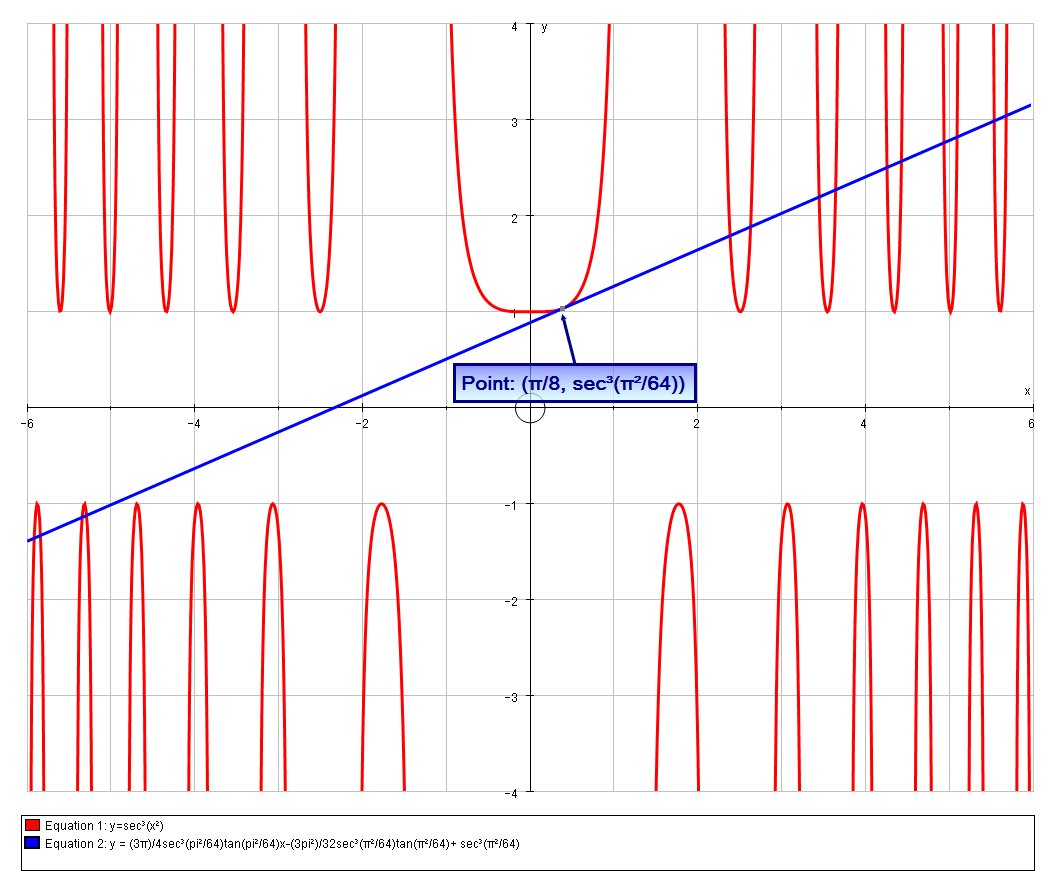
At
And the slope is given by
# = 6xsec^3(x^2)tan(x^2)#
At
# = (3pi)/4sec^3(pi^2/64)tan(pi^2/64)#
the equation of the line through
