What is the equation of the tangent line of # f(x)=(x-1)^2 # at # x=3 #?

Question

1006 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-12-15T17:40:01

#y=4x-8 #

The gradient of the tangent to a curve at any particular point is give by the derivative of the curve at that point.

so If #f(x)=(x-1)^2=x^2-2x+1# then differentiating wrt #x# gives us:

#dy/dx = 2x-2#

When #x=3 => y=9-6+1=4# (so #(3,4)# lies on the curve)
and #dy/dx=6-2=4#

So the tangent we seek passes through #(3,4)# and has gradient #4# so using #y-y_1=m(x-x_1)# the equation we seek is;

# \ \ \ \ \ y-4=4(x-3) #
# :. y-4=4x-12#
# :. \ \ \ \ \ \ \ y=4x-8 #

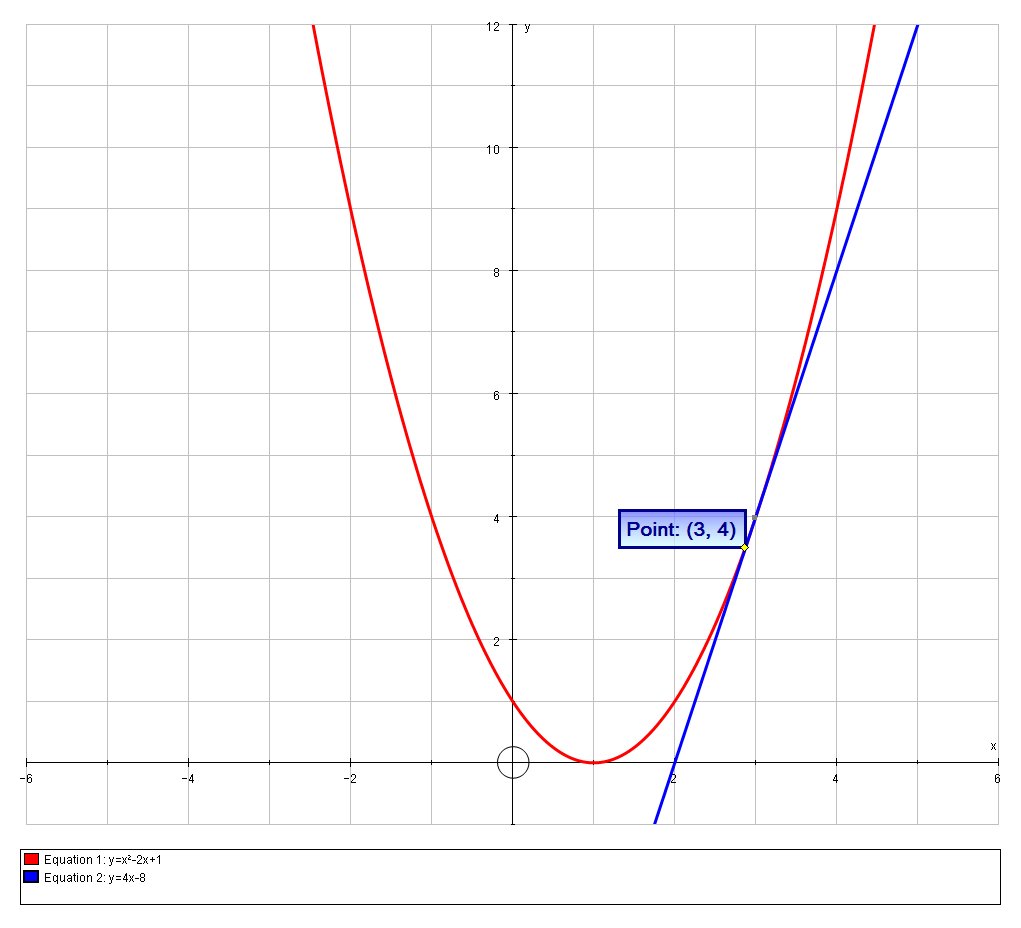
We can confirm this solution is correct graphically:
enter image source here