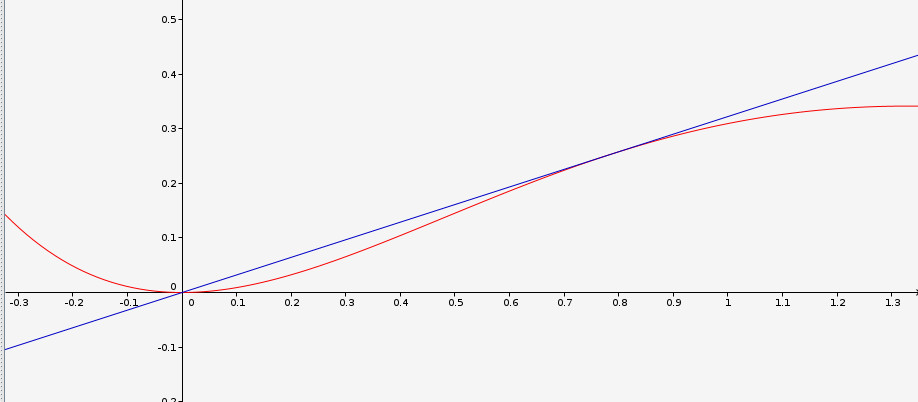
You would apply the formula
#(y-y_0)=m(x-x_0)#
to find the equation of the line, then you need #m# and #y_0#, since #x_0=pi/4#;
#m# is the derivative of the given function calculated at the given point #x_0#, then
#m=f'(pi/4)#
First, you would calculate #f'(x)# and the substitute #pi/4# in x:
#f'(x)=((sinx+xcosx)e^x-xsinxe^x)/e^(2x)=(cancele^x(sinx+xcosx-xsinx))/e^(cancel2x)=(sinx+xcosx-xsinx)/e^x#
Then
#m=f'(pi/4)=(sin(pi/4)+pi/4cos(pi/4)-pi/4sin(pi/4))/e^(pi/4)#
#m=(sqrt2/2+cancel(pi/4sqrt2/2)cancel(-pi/4sqrt2/2))/e^(pi/4)=sqrt2/2e^(-pi/4)#
On the other hand:
#y_0=f(x_0)=((pi/4)sin(pi/4))/e^(pi/4)=pi/4sqrt2/2e^(-pi/4)=(sqrt2pie^(-pi/4))/8#
Therefore the equation of the line is:
#y-(sqrt2pie^(-pi/4))/8=sqrt2/2e^(-pi/4)(x-pi/4)#
that's
#y=cancel((sqrt2pie^(-pi/4))/8)+sqrt2/2e^(-pi/4)xcancel(-(sqrt2pie^(-pi/4))/8))#
#y=sqrt2/2e^(-pi/4)x#