Calliing #p=(x,y,z)# and
#S->f(p) = p'Ap+c=0# where
#A = ((7,0,0),(0,-3,0),(0,0,1))#
and
#L->p = p_0 + lambda vec v# a line, the tangent planes to #S# containing #L# can be stated as:
#f(p_t) = 0#
#grad f(p_t) = vec n_t#
#<< p-p_t, vec n_t >> = 0#
#<< p_0+lambda vec v-p_t, vec n_t >> = 0# or
#<< p_0-p_t, vec n_t >> + lambda << vec v, vec n_t >> = 0#
This last relationship must be true for all #lambda# so it gives the two conditions
#<< p_0-p_t, vec n_t >> = 0#
#<< vec v, vec n_t >> = 0#
or resuming
#{(f(p_t)=0),(grad f(p_t) = vec n_t),(<< p_0-p_t, vec n_t >> = 0),(<< vec v, vec n_t >> = 0):}#
In the present case we have
#p_0 = (0,9/6,3)#
#vec v = (1,7/6,0)#
#vec n_t = 2Ap_t#
Solving for #p_t# we obtain two solutions
#p_t = (1,2,4)# and #p_t = (2,4,1)#
#vec n_t^1 = (14,-12,-8)# and #vec n_t^2 = (28,-24,-2)#
and consequently
#Pi_1 -> 21 + 7 x - 6 y - 4 z=0#
#Pi_2->42 + 28 x - 24 y - 2 z=0#
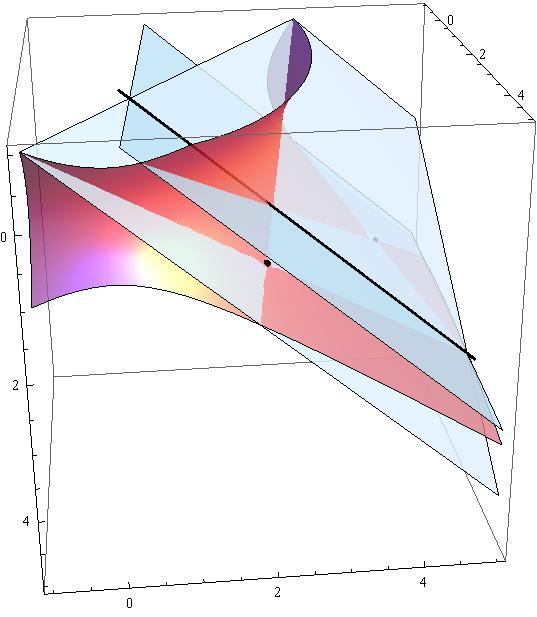
Attached the surface #S# in light pink, the two tangent planes in light blue, the line #L# in black and the two tangency points also in black