Question

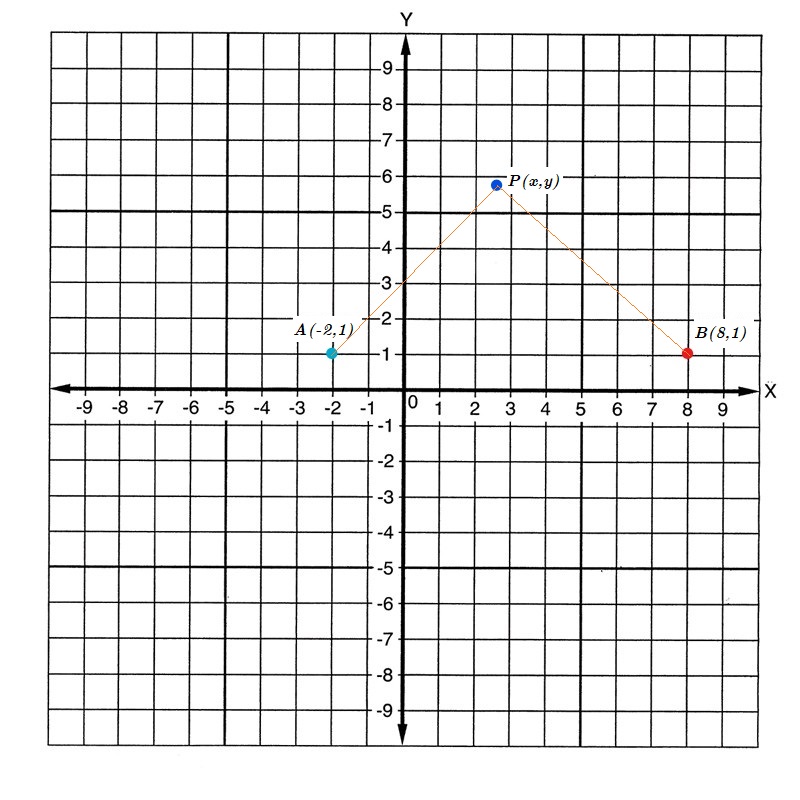
What is the equation of this curve with P given? The difference of the distance between P(x,y) and the points (-2,1) and (8,1) is 6.

Answer 1

`16x^2-9y^2-96x+18y-9=0`

Explanation:

let the point be `P(x,y)` (this will be general point).
Now according to question we have points
`A(-2,1)` and `B(8,1)`

also, the difference between the distances of the point is 6 units `i.e` `PA-PB=6`
or `PA=PB+6`
`=>PA^2=(PB+6)^2`
`=>PA^2=PB^2+12PB+36` `...(i)`

by distance formula we have
`PA=sqrt((x+2)^2+(y-1)^2)` and `PB=sqrt((x-8)^2+(y-1)^2`
`=>PA^2=(x+2)^2+(y-1)^2` and `PB^2=(x-8)^2+(y-1)^2`
putting these in `(i)`
we get
`(x+2)^2+cancel((y-1)^2)=(x-8)^2+cancel((y-1)^2)+12sqrt((x-8)^2+(y-1)^2)+36`

on solving we'll get
`16x^2-9y^2-96x+18y-9=0`
this represents a hyperbola,
graph{16x^2-9y^2-96x+18y-9=0 [-16.02, 16.02, -8.01, 8.01]}

this will be the equation of variable point `P(x,y)`
this is called the LOCUS of point `P`