What is the equation that connects pH and its effect on electric potential of an electrochemical cell?

Question

What is the equation that connects pH and its effect on electric potential of an electrochemical cell?

1 Answer

Impact of this question

45385 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-08-07T03:26:18

Well, first off, you'll need to begin with the Nernst equation:

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{R T}{n F} ln Q$ $E_(cell) = E_(cell)^@ - (RT)/(nF) lnQ$

where:

$E_{c e l l}$ $E_(cell)$ is the overall cell potential. $^{\circ}$ $""^@$ indicates $1 atm$ $"1 atm"$ and $25^{\circ} C$ $25^@ "C"$ .

$R$ $R$ and $T$ $T$ are known from the ideal gas law.

$n$ $n$ is the mols of electrons reportedly transferred in the redox reaction.

$F = {96485 C/mol e}^{-}$ $F = "96485 C/mol e"^(-)$ is Faraday's constant.

Note that $pH$ $"pH"$ only affects reactions that are done in acidic or basic media, i.e. those that contain significant $[H^{+}]$ $["H"^(+)]$ or $[{OH}^{-}]$ $["OH"^(-)]$ in solution already.

FROM THE PERSPECTIVE OF POURBAIX DIAGRAMS

The $pH$ $"pH"$ dependence is of both $E_{c e l l}^{\circ}$ $E_(cell)^@$ and $E_{c e l l}$ $E_(cell)$ , but again, only if the half-reactions or overall reactions contain $H^{+}$ $"H"^(+)$ or ${OH}^{-}$ $"OH"^(-)$ directly in them.

This can be seen in Pourbaix diagrams:

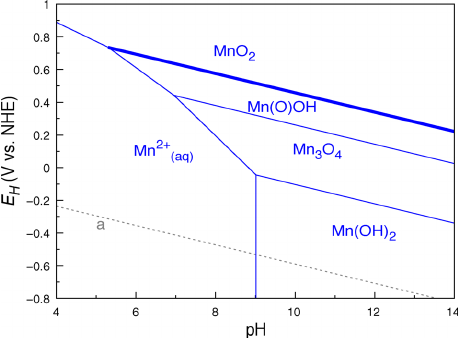
These are $E_{c e l l}^{\circ}$ $E_(cell)^@$ vs. $pH$ $"pH"$ diagrams.

Diagonal lines indicate an $E_{c e l l}^{\circ}$ $E_(cell)^@$ that is $pH$ $"pH"$ -dependent.
Vertical lines indicate $100 %$ $100%$ $pH$ $"pH"$ dependence.
Horizontal lines indicate $0 %$ $0%$ $pH$ $"pH"$ dependence.

As a cursory example, for a given $E_{c e l l}^{\circ}$ $E_(cell)^@$ , the ${Mn}_{3} O_{4} / Mn {(OH)}_{2}$ $"Mn"_3"O"_4//"Mn"("OH")_2$ half-reaction equilibrium in basic media is:

${Mn}_{3} O_{4} (s) + 4 H_{2} O (l) + 2 e^{-} ⇌ 3 Mn {(OH)}_{2} (s) + 2 {OH}^{-} (a q)$ $"Mn"_3"O"_4(s) + 4"H"_2"O"(l) + 2e^(-) rightleftharpoons 3"Mn"("OH")_2(s) + 2"OH"^(-)(aq)$

It shifts towards ${Mn}_{3} O_{4}$ $"Mn"_3"O"_4$ as $pH$ $"pH"$ increases (as we cross the diagonal line horizontally). Or, we could notice that when $pH$ $"pH"$ increases, $[{OH}^{-}]$ $["OH"^(-)]$ increases, promoting an equilibrium shift leftwards in accordance with Le Chatelier's principle. The reaction quotient $Q$ $Q$ changes accordingly away from $K$ $K$ , which changes $E_{c e l l}$ $E_(cell)$ accordingly.

FROM THE PERSPECTIVE OF THE NERNST EQUATION

Or, using the Nernst equation, we can investigate the $pH$ $"pH"$ dependence of the reaction quotient $Q$ $Q$ more thoroughly:

$Q = \frac{\prod_{i}^{N_{P}} {[P_{i}]}_{i}^{ν_{i}}}{\prod_{j}^{N_{R}} {[R_{j}]}_{j}^{ν_{j}}}$ $Q = \frac(prod_i^(N_P) [P_i]^(nu_i))(prod_j^(N_R) [R_j]^(nu_j))$ ,

where:

$N \prod k$ $prod_k^N$ indicates a multiplication of terms $1, 2, . . ., k, . . ., N$ $1, 2, . . . , k, . . . , N$ .

$i$ $i$ is the index of individual product concentrations $[P_{i}]$ $[P_i]$ being multiplied together.

$j$ $j$ is the index of individual reactant concentrations $[R_{j}]$ $[R_j]$ being multiplied together.

$ν_{k}$ $nu_k$ is the stoichiometric coefficient of the $k$ $k$ th reactant or product. Note that in general, $i \neq j$ $i ne j$ , meaning the number of products and reactants may differ.

So, we have the following conditions:

As the $pH$ $"pH"$ decreases, the solution is more acidic, so $10^{- pH} = [H^{+}]$ $10^(-"pH") = ["H"^(+)]$ increases and $10^{pH - 14} = [{OH}^{-}]$ $10^("pH" - 14) = ["OH"^(-)]$ decreases.

If $H^{+}$ $"H"^(+)$ is a product, $Q$ $Q$ therefore increases, and the nonstandard cell potential decreases.
If $H^{+}$ $"H"^(+)$ is a reactant, $Q$ $Q$ therefore decreases, and the nonstandard cell potential increases.
If ${OH}^{-}$ $"OH"^(-)$ is a product, $Q$ $Q$ therefore decreases, and the nonstandard cell potential increases.
If ${OH}^{-}$ $"OH"^(-)$ is a reactant, $Q$ $Q$ therefore increases, and the nonstandard cell potential decreases.

This is very situational, so it's not exactly possible to write one single equation for this, unless we make some assumptions.

PLAUSIBLE EQUATION

If the reaction does have an $H^{+}$ $"H"^(+)$ product or reactant, then... (and this is not in any textbook I know!)

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{R T}{n F} ln (Q^{*} \cdot {[H^{+}]}_{H^{+}}^{\pm ν_{H^{+}}^{+}})$ $E_(cell) = E_(cell)^@ - (RT)/(nF) ln (Q^"*"cdot["H"^(+)]^(pmnu_("H"^(+))))$

where:

$Q^{*}$ $Q^"*"$ is the $pH$ $"pH"$ -independent reaction quotient with $[H^{+}]$ $["H"^(+)]$ separated out.

$ν_{H^{+}}^{+}$ $nu_("H"^(+))$ is the stoichiometric coefficient of $H^{+}$ $"H"^(+)$ in the reaction.

In the $\pm$ $pm$ for $ν_{H^{+}}^{+}$ $nu_("H"^(+))$ , the $(+)$ $(+)$ indicates $H^{+}$ $"H"^(+)$ product, while the $(-)$ $(-)$ indicates $H^{+}$ $"H"^(+)$ reactant.

We could write $[H^{+}] = 10^{- pH}$ $["H"^(+)] = 10^(-"pH")$ to get:

$E_{c e l l} = E_{c e l l}^{\circ} - \frac{R T}{n F} {ln Q}^{*} - \frac{R T}{n F} ln ({[H^{+}]}_{H^{+}}^{\pm ν_{H^{+}}^{+}})$ $E_(cell) = E_(cell)^@ - (RT)/(nF) ln Q^"*" - (RT)/(nF) ln (["H"^(+)]^(pmnu_("H"^(+))))$

$= E_{c e l l}^{\circ} - \frac{R T}{n F} {ln Q}^{*} - \frac{\pm ν_{H^{+}}^{+} R T}{n F} ln (10^{- pH})$ $= E_(cell)^@ - (RT)/(nF) ln Q^"*" - (pmnu_("H"^(+))RT)/(nF) ln (10^(-"pH"))$

$= E_{c e l l}^{\circ} - \frac{R T}{n F} {ln Q}^{*} + pH \cdot \frac{\pm ν_{H^{+}}^{+} R T}{n F} ln 10$ $= E_(cell)^@ - (RT)/(nF) ln Q^"*" + "pH" cdot (pmnu_("H"^(+))RT)/(nF) ln 10$

Rearrange this further to get:

$E_{c e l l} - E_{c e l l}^{\circ} + \frac{R T}{n F} {ln Q}^{*} = pH \cdot \frac{\pm ν_{H^{+}}^{+} R T}{n F} ln 10$ $E_(cell) - E_(cell)^@ + (RT)/(nF) ln Q^"*" = "pH" cdot (pmnu_("H"^(+))RT)/(nF) ln 10$

$pH = \frac{E_{c e l l} - E_{c e l l}^{\circ} + \frac{R T}{n F} {ln Q}^{*}}{\frac{\pm ν_{H^{+}}^{+} R T}{n F} ln 10}$ $"pH" = (E_(cell) - E_(cell)^@ + (RT)/(nF) ln Q^"*")/((pmnu_("H"^(+))RT)/(nF) ln 10)$

$= \frac{\frac{n F}{R T} (E_{c e l l} - E_{c e l l}^{\circ}) + {ln Q}^{*}}{\pm ν_{H^{+}}^{+} ln 10}$ $= ((nF)/(RT)(E_(cell) - E_(cell)^@) + ln Q^"*")/(pmnu_("H"^(+))ln 10)$

Since $\frac{ln x}{log x} \approx 2.303$ $(lnx)/(logx) ~~ 2.303$ , we can approximate this as:

$color(blue)(barul|stackrel(" ")(" ""pH" ~~ ((nF)/(2.303RT)(E_(cell) - E_(cell)^@) + log Q^"*")/(pmnu_("H"^(+)))" ")|)$

keeping in mind that $Q^"*"$ neglects the $["H"^(+)]$ that would have been in the mass action expression, and that whether it was a product or reactant changes the sign of $nu_("H"^(+))$ .

Science

Math

Humanities

... and beyond

What is the equation that connects pH and its effect on electric potential of an electrochemical cell?

1 Answer

Related questions

Impact of this question