What is the equivalent to #sec[arcsin(x-1)]# in terms of an algebraic expression?

Question

#sec[arcsin(x-1)]#

9772 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-09T02:54:02

Please look below.

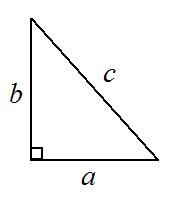
enter image source here

Let #theta = arcsin(x-1)# such that #theta# is the angle between #c# and #a# in the triangle above.

This means that #sin(theta) = x - 1#

Hence, #b = x-1# and #c = 1#

Using pythagoras shows that #a = sqrt(1-(x-1)^2)#

Now it can be easily seen that

#sec(theta) = 1/sqrt(1-(x-1)^2)#

Therefore
#sec[arcsin(x-1)] = 1/sqrt(1- (x-1)^2)#