Question

What is the first derivative test for critical points?

Answer 1

If the first derivative of the equation is positive at that point, then the function is increasing. If it is negative, the function is decreasing.

Explanation:

If the first derivative of the equation is positive at that point, then the function is increasing. If it is negative, the function is decreasing.
See Also:
http://mathworld.wolfram.com/FirstDerivativeTest.html

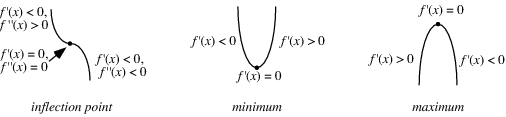
Suppose `f(x)` is continuous at a stationary point `x_0`.

1. If `f^'(x)>`0 on an open interval extending left from `x_0 and f^'(x)<0` on an open interval extending right from `x_0`, then `f(x)` has a local maximum (possibly a global maximum) at `x_0`.

2. If `f^'(x)<0` on an open interval extending left from `x_0 and f^'(x)>0` on an open interval extending right from `x_0, then f(x)` has a local minimum (possibly a global minimum) at `x_0`.

3. If `f^'(x)` has the same sign on an open interval extending left from `x_0` and on an open interval extending right from `x_0, then f(x)` has an inflection point at `x_0`.

Weisstein, Eric W. "First Derivative Test." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FirstDerivativeTest.html