What is the general equation for determining where a projectile launched from the ground will land?
1 Answer
This is a repeat question. However, since a general expression is to be worked out so see details below.
Range
Explanation:
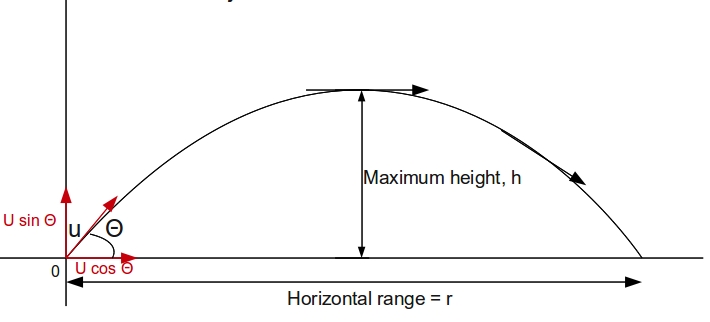
Let the projectile be lunched with initial velocity
Distance traveled horizontally in time of flight t gives us the Horizontal Range
Assuming zero air friction, and noticing that there is no acceleration in the horizontal direction we obtain
To obtain time of flight
It is observed that the projectile will rise initially, attain maximum height and then fall down due to gravity.
Using the formula
Take
We obtain
Substituting value of t in expression (1)
