Question

What is the graph of `y=cos(x-pi/2)`?

Answer 1

First, the graph of `y=cos(x-pi/2)` will have some characteristics of the regular cosine function.
I also use a general form for trig functions: `y = a cos(b ( x - c)) + d` where |a| = amplitude, `2pi/|b|` = period, x = c is the horizontal phase shift, and d = vertical shift.

1) amplitude = 1 since there is no multiplier other than "1" in front of the cosine.

2) period = `2pi` since the regular period of cosine is `2pi`, and there is no multiplier other than a "1" attached to the x.

3) Solving `x - pi/2=0` tells us that there is a phase shift (horizontal translation) of `pi/2` to the right.

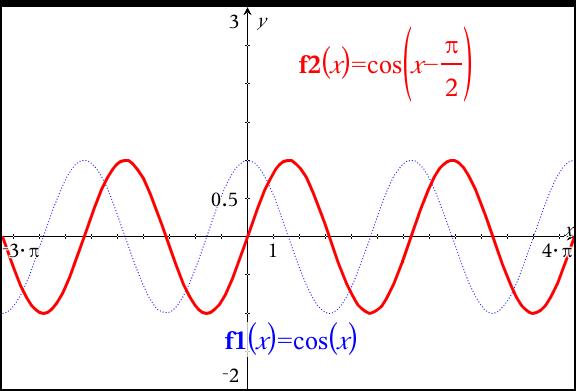
The bright, red graph is your graph!
Compare it to the dotted, blue graph of cosine. Do you recognize the changes itemized above?