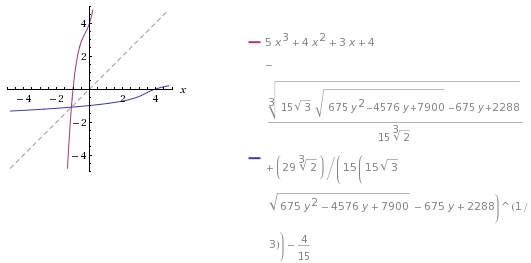Question

What is the inverse function of `f(x) =5x^3 + 4x^2 + 3x + 4`?

Answer 1

`x=5y^3+4y^2+3y+4`

Explanation:

The simplest way to write the inverse function is to write `y` in place of `f(x)` and switch all the `x`s with `y`s and the `y` with `x`, giving:

`x=5y^3+4y^2+3y+4`

This can be written explicitly (in terms of `y`), but it uses the incredibly cumbersome cubic formula and is overall unhelpful. But, for the sake of interest, it's as follows:

`x=-(15 sqrt(3) sqrt(675 y^2-4576 y+7900)-675 y+2288)^(1/3)/(15 (2^(1/3)))+(29 (2^(1/3)))/(15 (15 sqrt(3) sqrt(675 y^2-4576 y+7900)-675 y+2288)^(1/3))-4/15`

Graph: