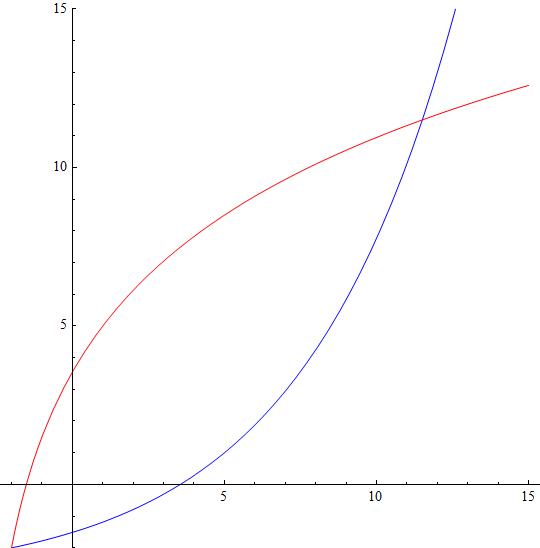
What is the inverse of the function #f(x) = 7log_4(x+3) - 2#? It is #7log_4 (x+3) - 2#, if that clears any confusion.

Question

2150 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-05T17:01:20

#g(x) = 4^{(x+2)/7}-3#

Calling #f(x) = 7log_4(x+3) - 2# we have

#f(x) = log_4((x+3)^7/4^2) = y#

Now we will proceed to obtain #x = g(y)#

#4^y = (x+3)^7/4^2# or
#4^{y+2} = (x+3)^7#
#4^{(y+2)/7}=x+3# and finally
#x = 4^{(y+2)/7}-3 = g(y) = (g@f)(x)#

So #g(x) = 4^{(x+2)/7}-3# is the inverse of #f(x)#

Attached a plot with #f(x)# in red and #g(x)# in blue.

enter image source here