Question

What is the limit of `limxto1(sqrt(x+3)-2)/(x-1)`?

Answer 1

I got: `1/4`.

Explanation:

Have a look:

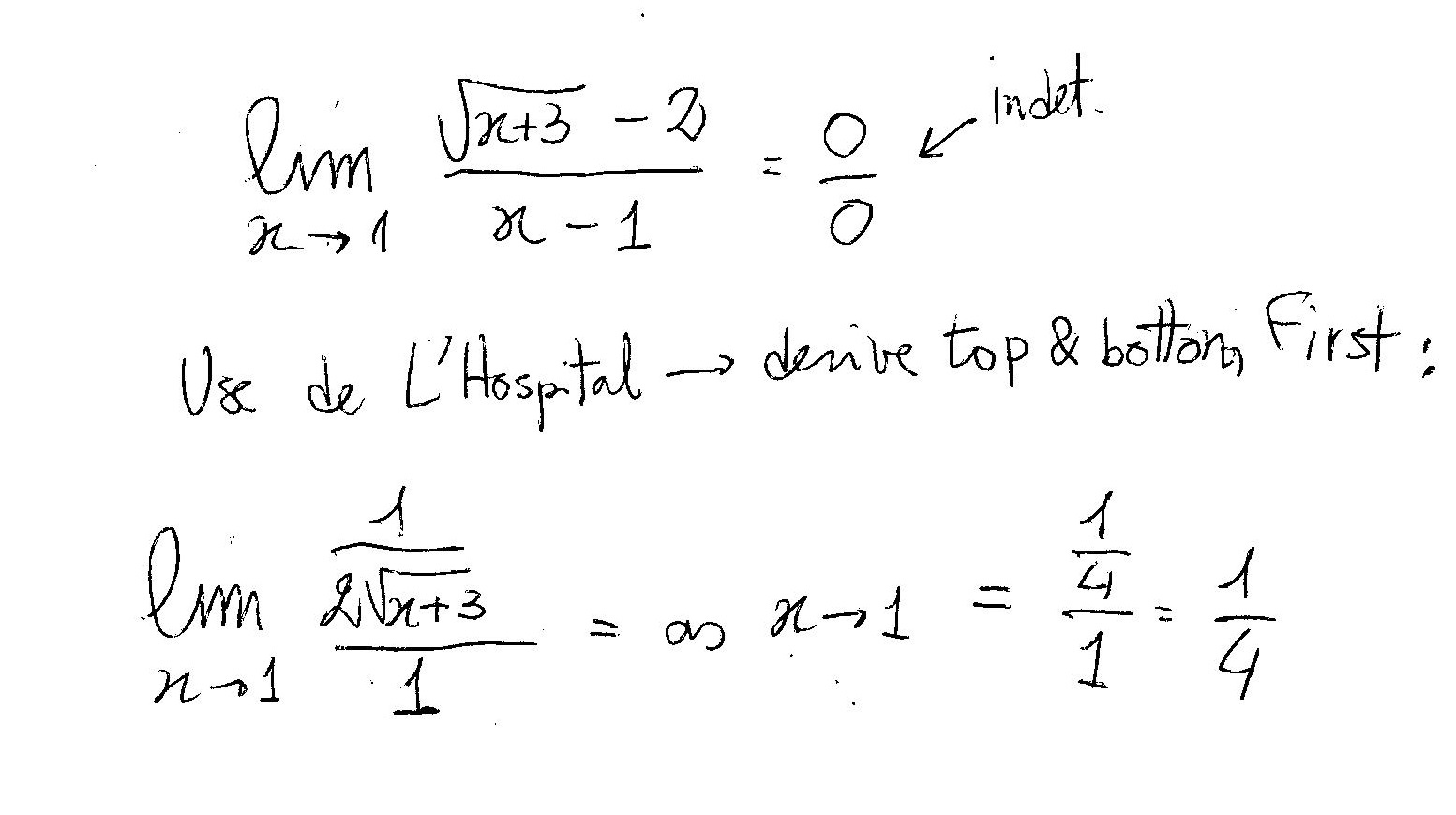
we could also try this:
Let us multiply top and bottom by `sqrt(x+3)+2`, we get:
`lim_(x->1)((sqrt(x+3)-2)/(x-1))(sqrt(x+3)+2)/(sqrt(x+3)+2)`
we would get:
`lim_(x->1)((x+3)-4)/((x-1)(sqrt(x+3)+2))`
`lim_(x->1)cancel((x-1))/(cancel((x-1))(sqrt(x+3)+2))`
as `x->1` we get:
`lim_(x->1)1/((sqrt(x+3)+2))=1/4`