What is the linear approximation of a function?
1 Answer
The linear approximation of a function f(x) is the linear function L(x) that looks the most like f(x) at a particular point on the graph y = f(x). This depends on what point (a, f(a)) you want to focus in on. Spoiler Alert: It's the tangent line at that point! The tangent line matches the value of f(x) at x=a, and also the direction at that point.
Let's find the equation of the tangent line, then. The limit definition of the derivative at a point tells us that the difference quotient
So
meaning that the equation of the tangent line at x=a is
That's your linear approximation, brought to you by calculus \and dansmath!/
P.S. This is the first two terms of the Taylor Series; with more terms you can approximate a function at any point with higher degree polynomials!
One of the reasons to use linear approximations is that we can estimate an answer without the use of a calculator because it is usually a simple multiplication/division and addition. The other thing to note is the approximation is better the closer you are to
Let's look at estimating
#f(x)=sqrt(x)#
#f'(x)=1/(2sqrt(x))#
We want to choose an
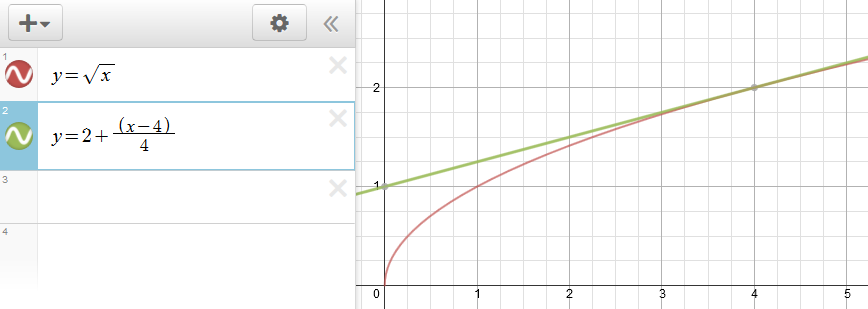
#L(x)=f(4)+f'(4)(x-4)#
#=2+1/4(x-4)#
So, we evaluate for the desired value:
#L(4.01)=2+1/4(4.01-4)#
#=2+.01/4#
#=2.0025# done without a calculator (mathamagics)!
This is a very good estimate because