-what is the magnitude of tension in the rope? -find the horizontal and vertical components of the force exerted at A on the lamina by the wall.
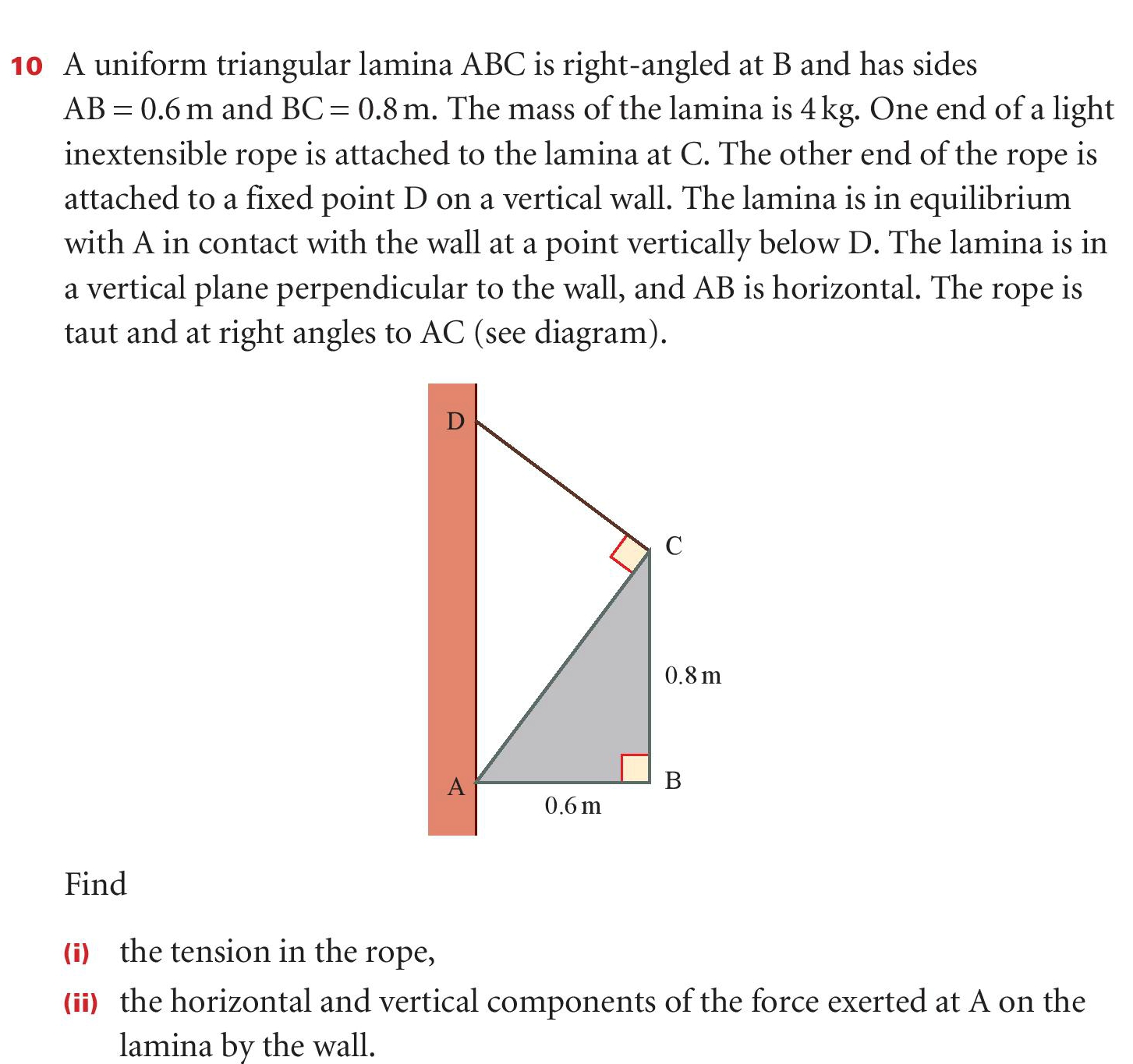
A uniform triangular lamina ABC is right-angled at B and has sides
AB = 0.6 m and BC = 0.8 m. The mass of the lamina is 4 kg. One end of a light
inextensible rope is attached to the lamina at C. The other end of the rope is
attached to a fixed point D on a vertical wall. The lamina is in equilibrium
with A in contact with the wall at a point vertically below D. The lamina is in
a vertical plane perpendicular to the wall, and AB is horizontal. The rope is
taut and at right angles to AC
Find
(i) the tension in the rope,
(ii) the horizontal and vertical components of the force exerted at A on the
lamina by the wall.
A uniform triangular lamina ABC is right-angled at B and has sides
AB = 0.6 m and BC = 0.8 m. The mass of the lamina is 4 kg. One end of a light
inextensible rope is attached to the lamina at C. The other end of the rope is
attached to a fixed point D on a vertical wall. The lamina is in equilibrium
with A in contact with the wall at a point vertically below D. The lamina is in
a vertical plane perpendicular to the wall, and AB is horizontal. The rope is
taut and at right angles to AC
Find
(i) the tension in the rope,
(ii) the horizontal and vertical components of the force exerted at A on the
lamina by the wall.

1 Answer
See below.
Explanation:
For a homogeneous lamina, the triangle's center of mass is given by
Now momentum equilibrium
and static resultant equilibrium
Here
After substituting values on
giving
or

