What is the maximum value that the graph of #f(x)=4x^2-24x+1#?
1 Answer
There is no maximum for this function. Just minimum (3,35), the function is convex.
Explanation:
Given
As
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If you wanted to find the minimum, this could be done by taking the derivative and noting that the derivative will be equal to zero at extrema.
However, this may just be a trick question to see if you will answer with the minimum value without considering that the extreme point is a minimum and not the maximum.
Further details
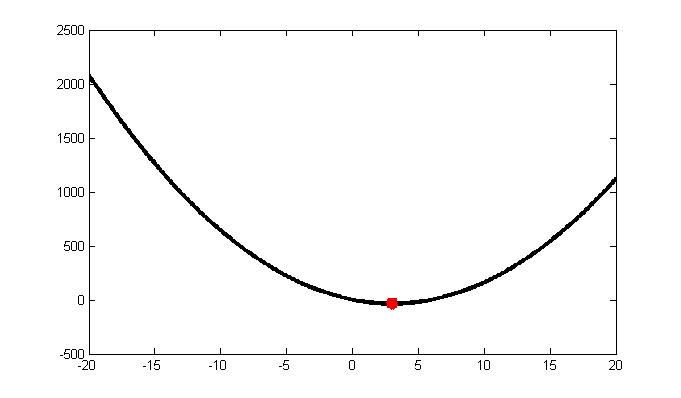
The vertex s given by:
Advanced (calculus needed)
The first derivative is:
To find
The second derivative:
See for more: http://mathworld.wolfram.com/ConvexFunction.html, https://en.wikipedia.org/wiki/Parabola#Coordinates_of_the_vertex, http://hotmath.com/hotmath_help/topics/vertex-of-a-parabola.html

