What is the next number in this sequence 1, 1, 3, 2, 4, 6, 5, 25?
3 Answers
Explanation:
This is not a very mathematically significant kind of sequence.
The steps are:
1) Square the previous term.
2) Add 2 to the previous term.
3) Subtract 1 from the previous term.
(repeat)
Is there a single algebraic formula to describe this iterative process?
Consider
This has the property that
Then we can write:
This can be simplified, but it helps to have it in this formulation so you can understand how it works.
When
When
When
So we use these to pick out each of the three rules cyclically.
anything you want it to be
Explanation:
Since the given sequence is obviously not arithmetic, geometric, nor exponential
one (?obvious?) solution would be to generate a polynomial function with these values as the function values for their position in the sequence:
and so on.
Given a set of
Explanation:
As Alan says, you can construct a polynomial of degree
Let's look at the differences and differences of differences...
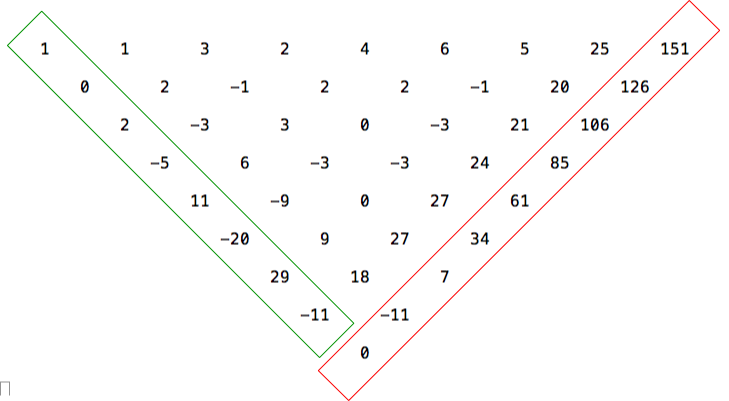
We can use the first element of each row of differences (as enclosed by the green rectangle) to construct a polynomial for the sequence:
If a sequence was really constructed using a polynomial then you would expect to encounter a row of
In our case that does not happen, but see what happens when we add an extra row and reconstruct the next term of the sequence. It's somewhat easier than substituting
So for the polynomial of lowest degree that generates the sequence as given, the next term would be

