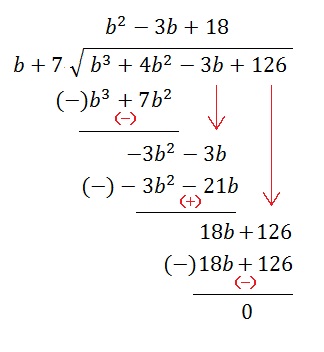What is the quotient of #b^3 + 4b^2 – 3b + 126# by b+7?

Question

3521 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-04-10T15:11:36

#b^2-3b+18#

Use long division, as used for integers, to find the quotient.

The divisor is #b+7#.
Look at the first term of the dividend, i.e. #b^3#.

What should be multiplied to #b# (of the divisor) to get the first term of the dividend, i.e. #b^3#?

#bxx b^2=b^3#
Therefore, #b^2# becomes the first term of the quotient.

Now, #b^2 xx (b+7)=b^3 + 7b^2#
Write it below the corresponding terms of the dividend and subtract.

We are now left with #-3b^2-3b+126#.

Repeat.

enter image source here