Question

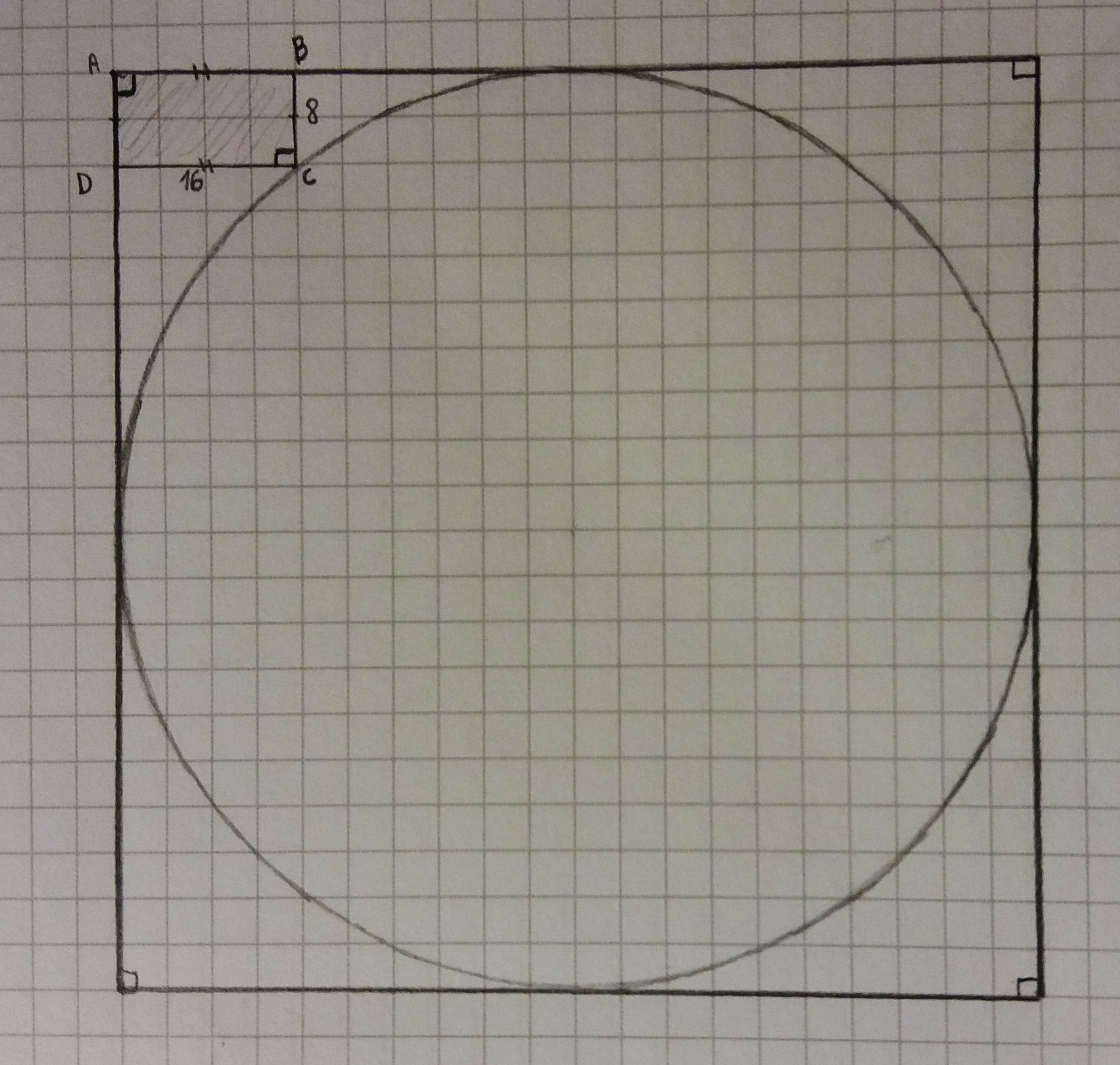
What is the radius of the circle?

`AB=CD=16`
`BC=DA=8`

Answer 1

4 squares = 16 units; therefore 1 square = 2 units

There diameter of the circle is 20 squares. There for the radius of the circle is 10 squares

`10"squares" xx (2units)/"square" = 20"units"`

Answer 2

`r=40`

Explanation:

note some of the simplification is omitted and is left for the reader to verify.

consider the upper left hand quadrant

consider the triangle `OAB`

from the diagram it can be seen that

`OA=r-16`

`AB=r-8`

we have aright angled triangle and so apply Pythagoras' theorem

`r^2=(r-8)^2+(r-16)^2`

`r^2=r^2-16r+64+r^2-32r+256`

this simplifies to

`r^2-48r+320=0`

factorising

`(r-40)(r-8)=0`

either

`r=8`

this cannot be a solution as seen from the diagram

or

`r=40`