What is the range of #g(x)=6^x-3#?
1 Answer
Apr 17, 2018
Explanation:
as
Notice when
as
So the range of the function is:
The graph of
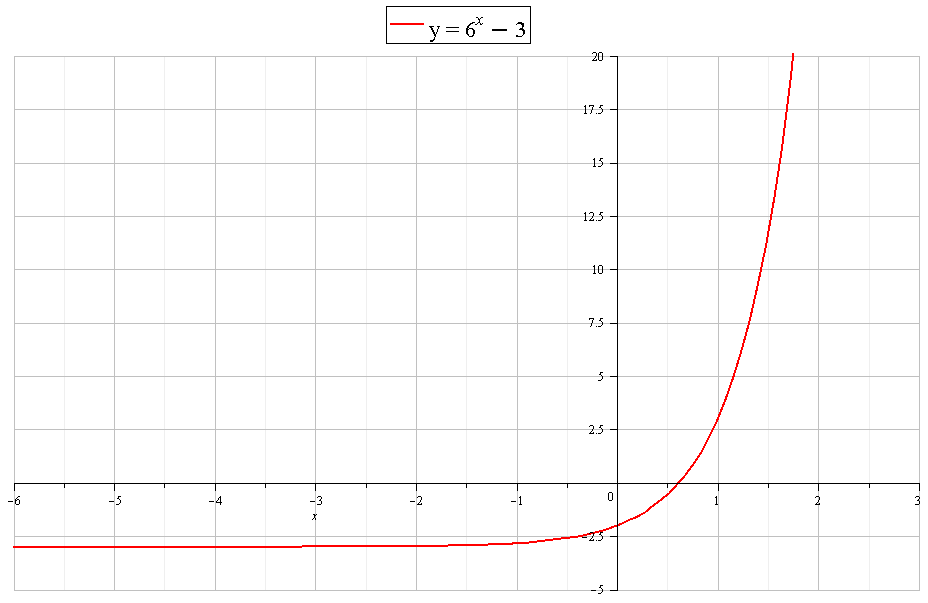
as
Notice when
as
So the range of the function is:
The graph of
