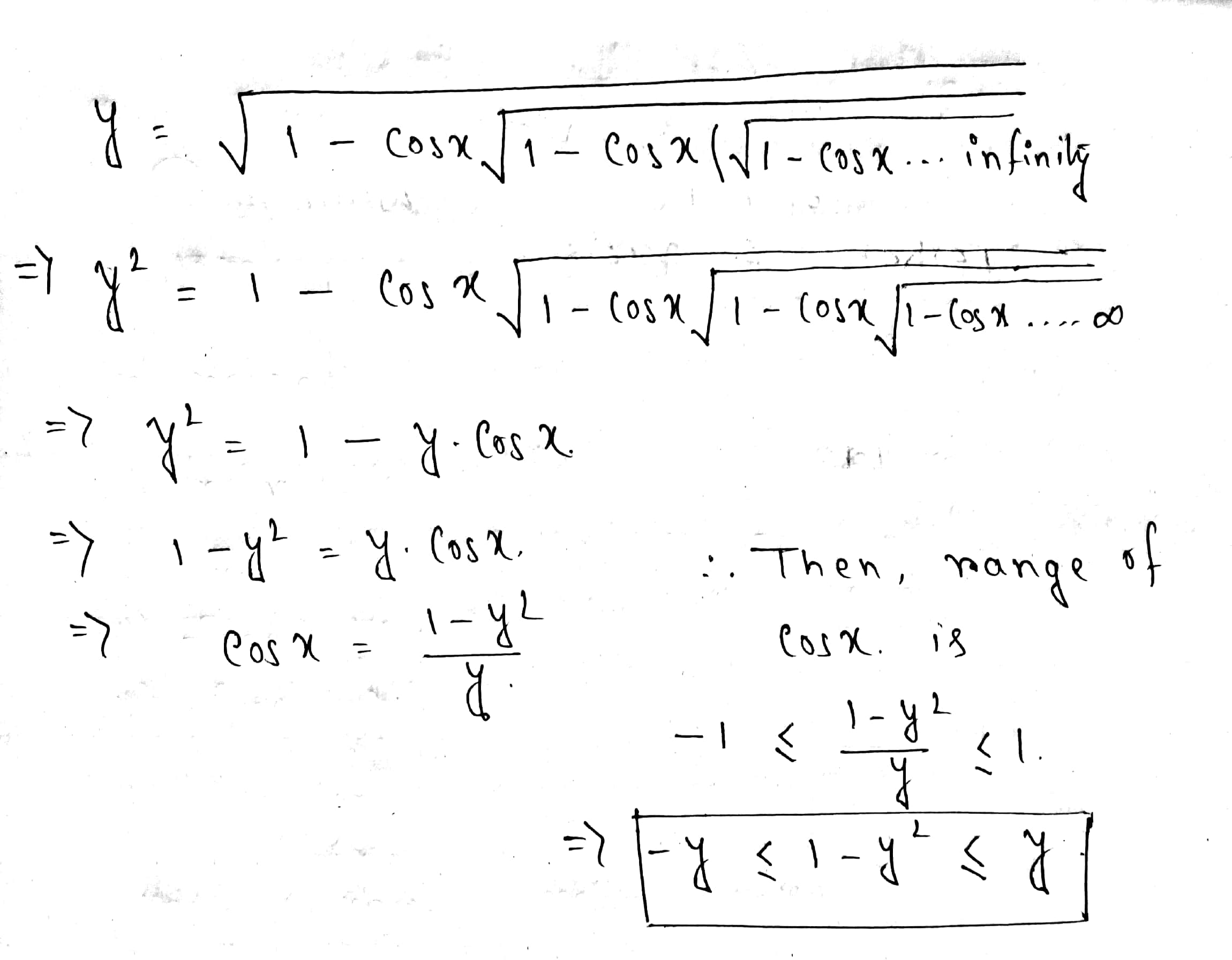What is the range of the function #y=sqrt(1-cosxsqrt(1-cosx(sqrt(1-cosx ......oo# ?
3 Answers
I need double-check.
Explanation:
Explanation:
Given:
#y = sqrt(1-cos xsqrt(1-cos xsqrt(1-cosxsqrt(...))))#
write
#y = sqrt(1-tsqrt(1-tsqrt(1-tsqrt(...))))#
Square both sides to get:
#y^2 = 1-tsqrt(1-tsqrt(1-tsqrt(...))) = 1-ty#
Add
#y^2+ty-1 = 0#
This quadratic in
#y = (-t+-sqrt(t^2+4))/2#
Note that we need to choose the
So:
#y = (-t+sqrt(t^2+4))/2#
Then:
#(dy)/(dt) = -1/2+t/(2sqrt(t^2+4))#
This is
#t/sqrt(t^2+4) = 1#
That is:
#t = sqrt(t^2+4)#
Squaring both sides:
#t^2 = t^2+4#
So the derivative is never
So the maximum and minimum values of
When
#y = (1+sqrt(5))/2#
When
#y = (-1+sqrt(5))/2#
So the range of
#[(-1+sqrt(5))/2, (1+sqrt(5))/2]#
graph{(y-(-(cos x)+sqrt((cos x)^2+4))/2) = 0 [-15, 15, -0.63, 1.87]}
See below.
Explanation:
We have
Here
Now
then the feasible limits are
NOTE
With
we have that