Question

What is the range of the stone if it is released when the sling is inclined at 30.0° with the horizontal at A?

Answer 1

Please see below

Explanation:

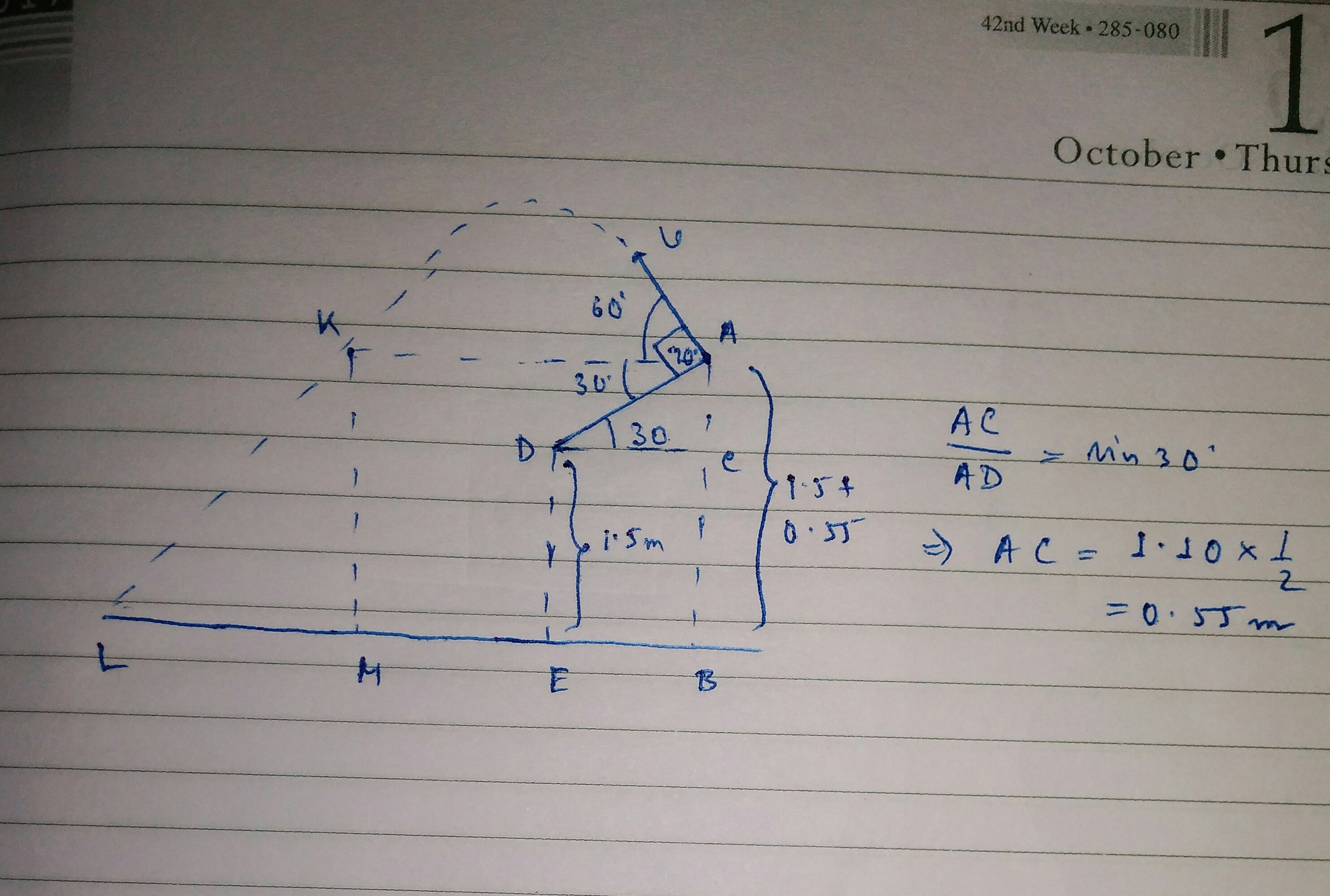
So,we can calculate the length `AK=BM` from the the diagram,as the range of projectile motion,using the formula, `R= (u^2 sin 2 theta )/g = (1^2 sin 120)/g=0.087 m`

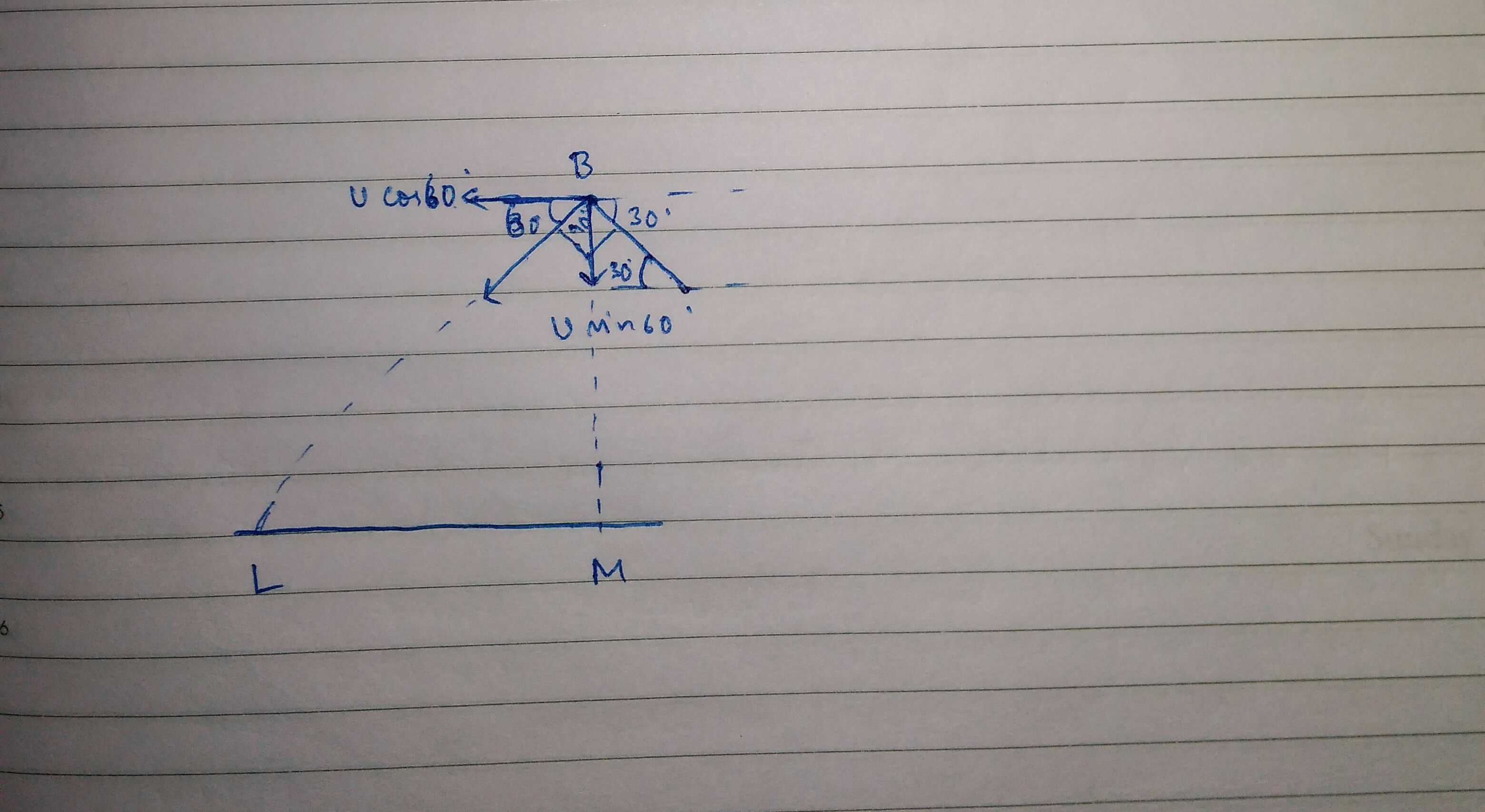
Now,when the stone will return to point `K` it will have the same vertical component of velocity that it had at point `A`,but it will be directed downwards,

So,at point `K` downward component of velocity = `v sin 60 = sqrt(3)/2`

Now,if it takes time `t` to reach the ground,then considering only vertical motion,we can write,

`2.05 = sqrt(3)/2 t + 1/2 g t^2` (using, `s= ut +1/2 g t^2`)

So, `t=0.55 s`

So,in that time if the stone horizontally went from `M` to `L`,then, `ML = v cos 60 *t= 1/2 *0.55=0.275 m` (using, `s=vt`, as horizontal component of velocity remains unchanged)

So,range of motion = `BM + ML = 0.087 + 0.275=0.362m`

Now,you can easily work out the 2nd part of the question, here your range will be only, `LM` of the 1st problem's picture.

Here is a diagram to help you,