Question

What is the rate of change?

For the function y = 2x^2-2x estimate the rate of change of y with respect to x when x = 1.5

Answer 1

`color(blue)(4)`

Explanation:

`y=2x^2-2x`

To find the rate of change we need to find the derivative of `2x^2-2x`, this is sometimes referred to as the gradient function.

So we are looking for:

`dy/dx(2x^2-2x)`

`dy/dx(2x^2-2x)=dy/dx(2x^2)+dy/dx(-2x)`

We can use the power rule to find this:

`dy/dx(ax^n)=n*ax^(n-1)`

So:

`dy/dx(2x^2)=2*2x^(2-1)=4x`

`dy/dx(-2x)=1*-2x^(1-1)=-2`

Then:

`dy/dx(2x^2-2x)=4x-2`

We now plug into this the value `x=1.5`

`4x-2`

`4(1.5)-2=color(blue)(4)`

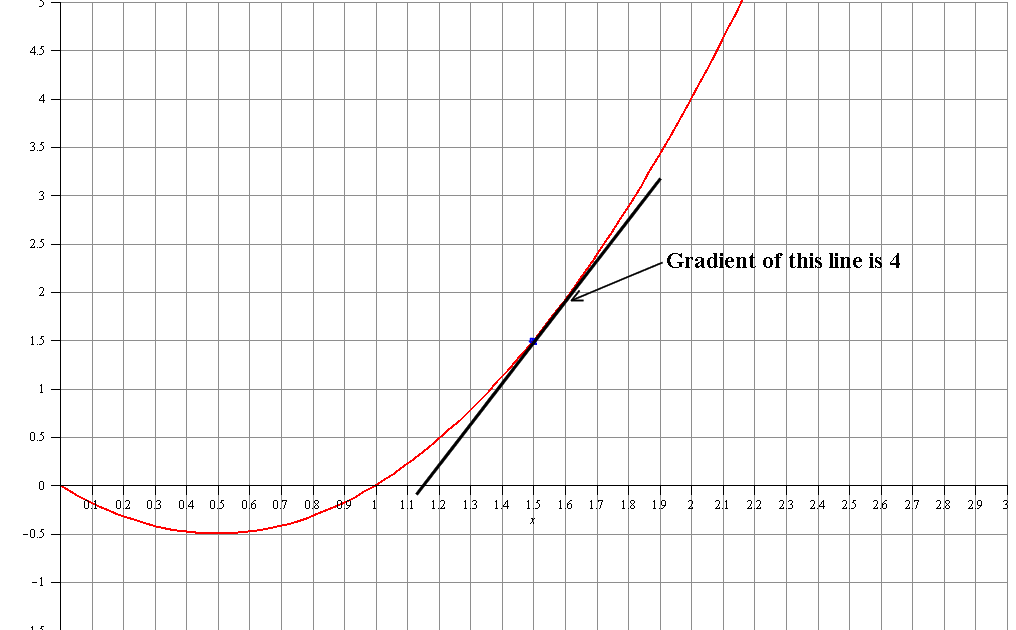
So the rate of change of y in respect of x is 4

This is just the gradient of a tangent line drawn at `x=1.5`

GRAPH: