What is the relationship among amplitude, crest, and trough?
1 Answer
The relationship is
Explanation:
In general, a wave can be defined as the periodic change of one (dependent variable), y, with another (independent variable) x.
In physics, the dependent variable y may be a physical quantity like pressure, voltage, height and the independent variable may be a physical quantity like time, space or something related (but doesn’t have to be).
The amplitude is the difference between the equilibrium value (of the dependent variable) and the maximum value the dependent quantity will take over one period.
Let’s take a concrete example
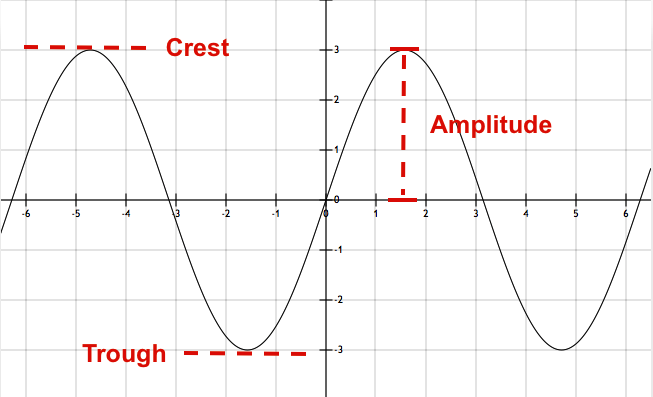
Since the crest of the wave is defined as the highest value (e.g.
So, in this case,

