What is the slope of the line normal to the tangent line of #f(x) = e^(x^2-1)+2x-2 # at # x= 1 #?

Question

1588 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-16T04:28:26

#y=-1/82.34x+22.09#

Given

#y=e^(x^2-1)+2x-2#

At #x=2#

#y=2.71828^(2^2-1)+2(2)-2#
#y=2.71828^3+4-2#
#y=20.085+2=22.085#

At Point #(2, 22.085)# There is a tangent to the curve.
Look at the graph
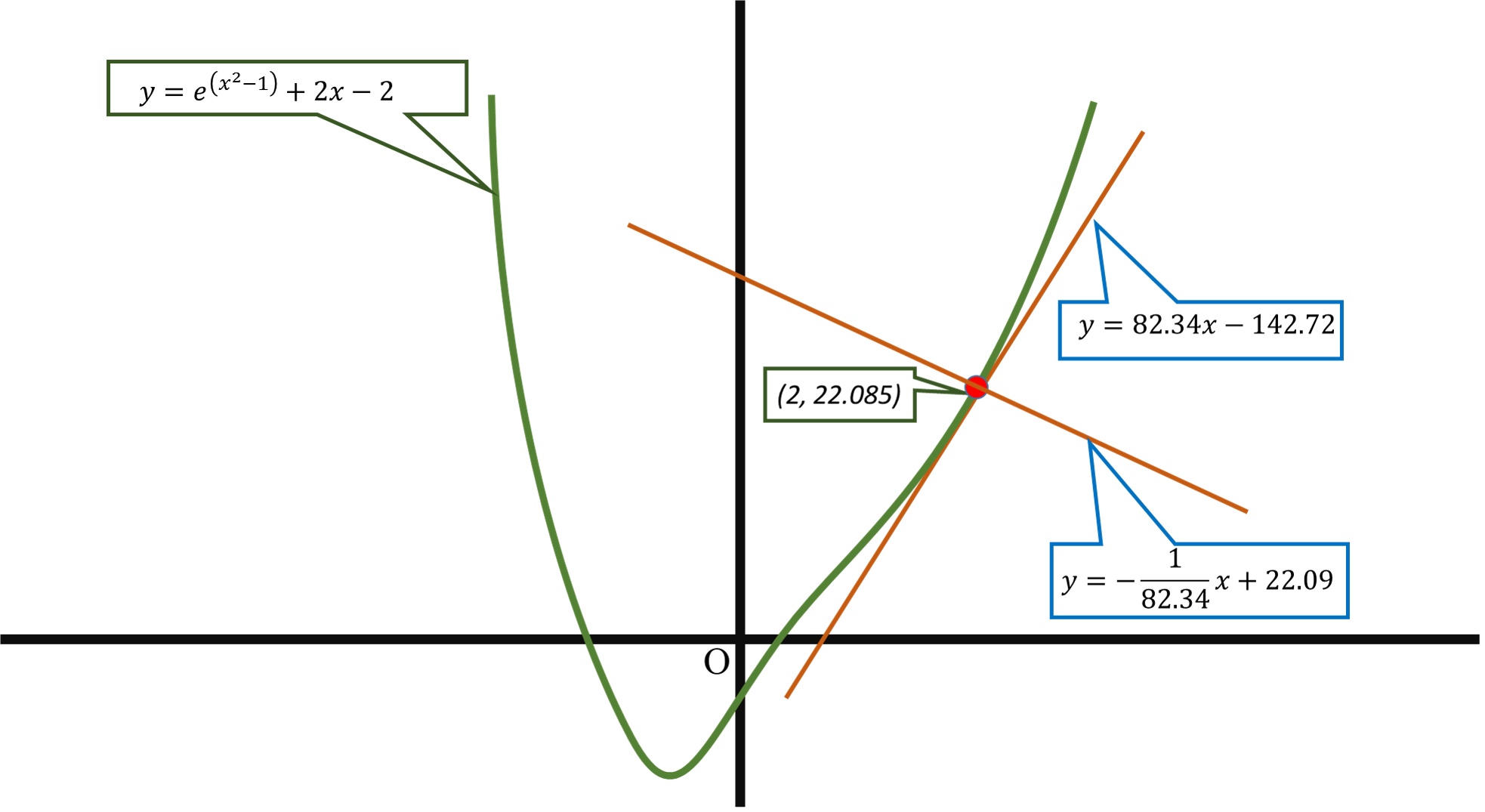
enter image source here

The slope of the tangent is equal to the slope of the given curve.

The slope of the given curve is-

#dy/dx=2xe^(x^2-1)+2#

At #x=2# the slope of the curve is

#dy/dx=2(2)(2.71828^3)+2#
#dy/dx=4xx 20.085+2#
#dy/dx=82.34#

The slope of the tangent #m_1=82.34#

The slope of the normal is #m_2=-1xx1/82.34=(-1)/82.34#

The equation of the Normal is -

#y=m_2x+c#
#22.085=-1/82.34(2)+c#
#22.085+1/82.34=c#
#22.09=c#

#y=-1/82.34x+22.09#