Question

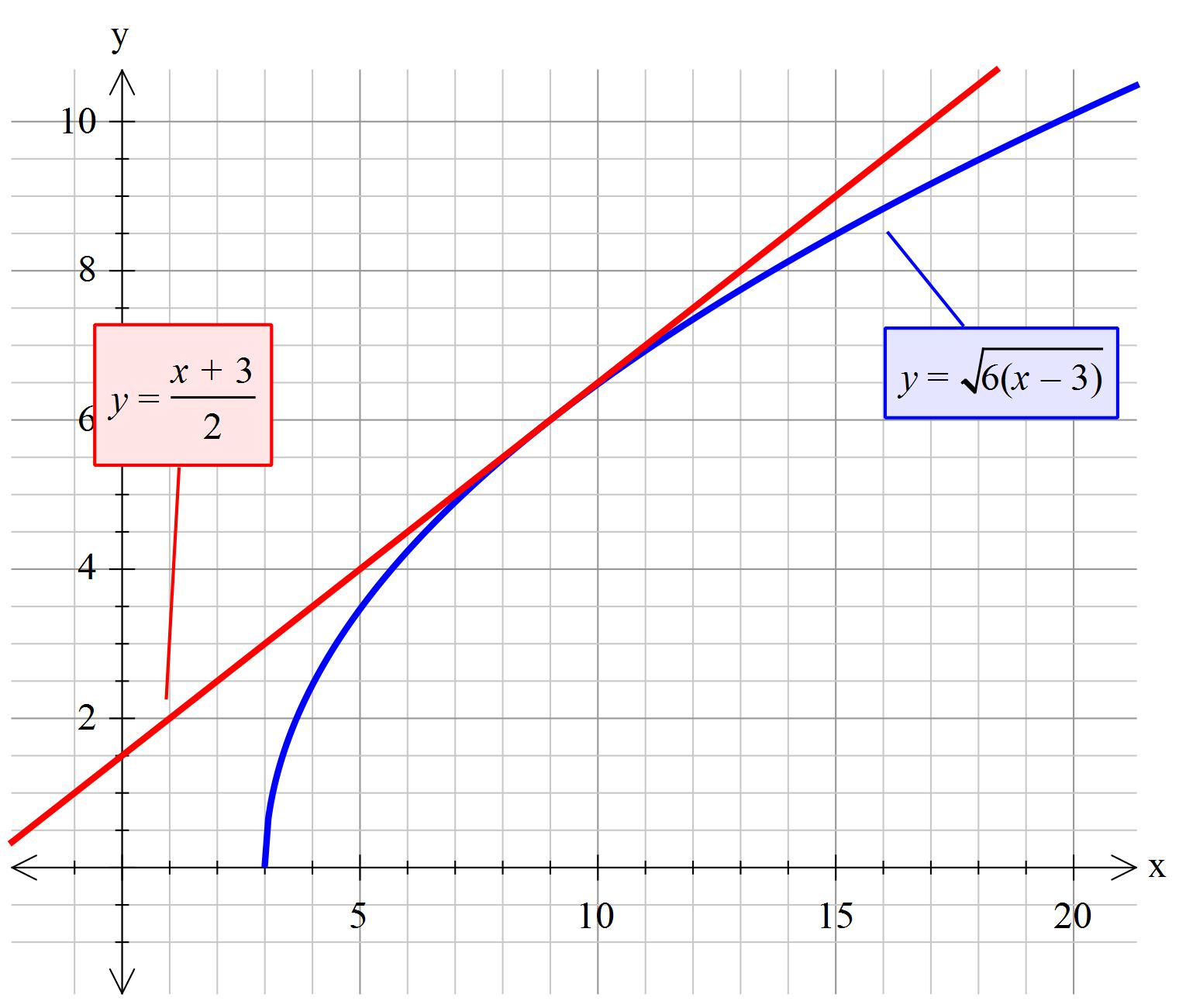
What is the solution to the following system of equations?:# log6 + log(x-3) = 2logy, 2y - x = 3#

Answer 1

`x=9`

Explanation:

Given:
`" "log(6)+log(x-3)=2log(y)`..................................(1)
`" "2y-x=3`...............................................(2)
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Consider equation (1)")`

Adding loges means that the source numbers are multiplied

`=>" "log(6)+log(x-3) -= log[6(x-3)]`

Also `2log(y) -= log(y^2)`

So equation (1) can be rewritten as:

`" "log(6(x-3))=log(y^2)`

If the logs are equal to each other then the source values are also equal to each other.

`color(blue)(=>" " 6(x-3)=y^2)" ".........................(1_a)`

'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Consider equation (2)")`

`2y-x=3`

Add `x` to both sides

`2y=x+3`

Divide both sides by 2

`color(blue)(y=(x+3)/2)" "........................(2_a)`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

We still have two variable so we need to 'get rid' of one of them.
This can be achieved if we equate them to each other through y. To be able to do this the y's need to be the same for each.

Square both sides of equation `(2_a)` giving

`y^2=((x+3)^2)/4" "......................(2_b)`

Equate `(2_b)" to "(1_a)` through `y^2`

`" "((x+3)^2)/4 = y^2 =6(x-3)`

`" "((x+3)^2)/4 =6(x-3)`

`" "x^2+6x+9=24x-72`

`" "x^2-18x+81=0`

`" "(x-9)^2=0`

`x=+9`