What is the standard form equation of the parabola with a vertex at (0,0) and directrix at x= -2?

Question

4070 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-30T16:54:04

#x = 1/8y^2#

Please observe that the directrix is a vertical line, therefore, the vertex form is of the equation is:

#x = a(y-k)^2+h" [1]"#

where #(h,k)# is the vertex and the equation of the directrix is #x = k - 1/(4a)" [2]"#.

Substitute the vertex, #(0,0)#, into equation [1]:

#x = a(y-0)^2 + 0#

Simplify:

#x = ay^2" [3]"#

Solve equation [2] for "a" given that #k = 0# and #x = -2#:

#-2 = 0 - 1/(4a)#

#4a = 1/2#

#a = 1/8#

Substitute for "a" into equation [3]:

#x = 1/8y^2 larr# answer

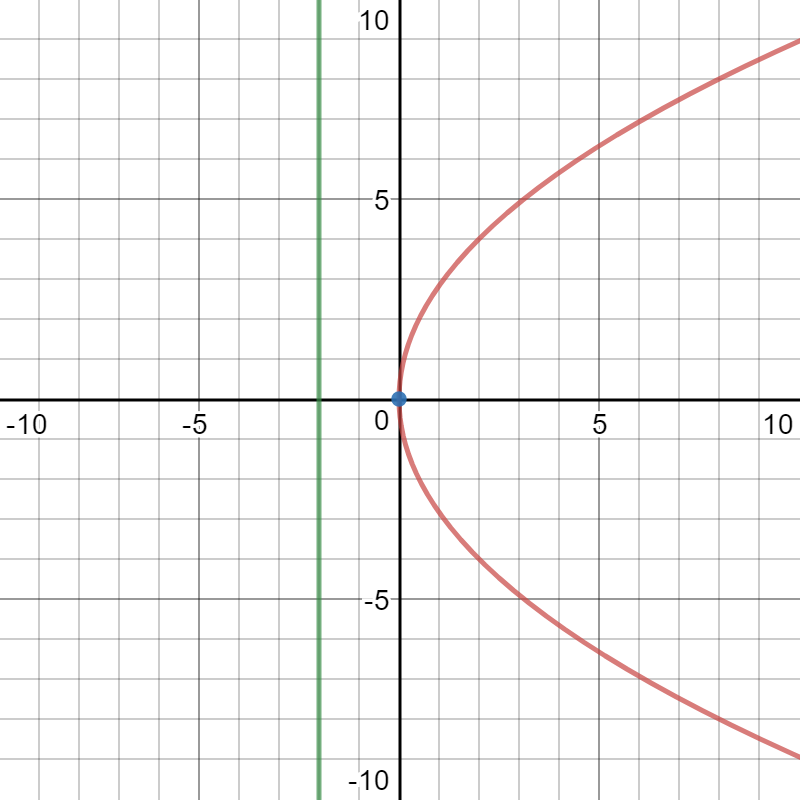
Here is a graph of the parabola with the vertex and the directrix:

Desmos.com