What is the standard form of the equation of the parabola with a directrix at x=9 and a focus at (8,4)?
1 Answer
The standard form is:
Explanation:
Because the directrix is a vertical line, one knows that the vertex form of the equation for the parabola is:
where
The x coordinate of the vertex halfway between the directrix and the focus :
Substitute into equation [1]:
The y coordinate of the vertex is the same as the y coordinate of the focus:
Substitute into equation [2]:
The value of
Substitute into equation [3]:
This is the vertex form:
Expand the square:
Use the distributive property:
Combine like terms:
Here is a graph of the standard form, the focus, the vertex, and the directrix:
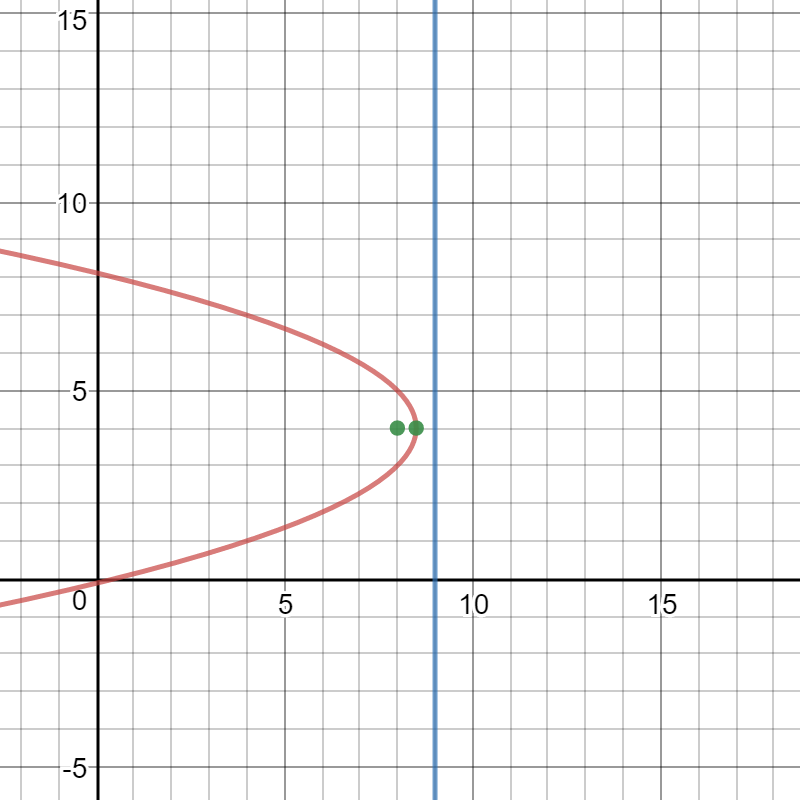 www.desmos.com/calculator
www.desmos.com/calculator
