What is the standard form of the equation of the parabola with a focus at (6,3) and a directrix of #y= 1#?

Question

837 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-07-27T07:04:26

#y=1/8x^2-3/2x+15/2#

Given -

Vertex #(6, 3)#
Directrix #y= 1#

Parabola opens up.
Its vertex is not at the origin.
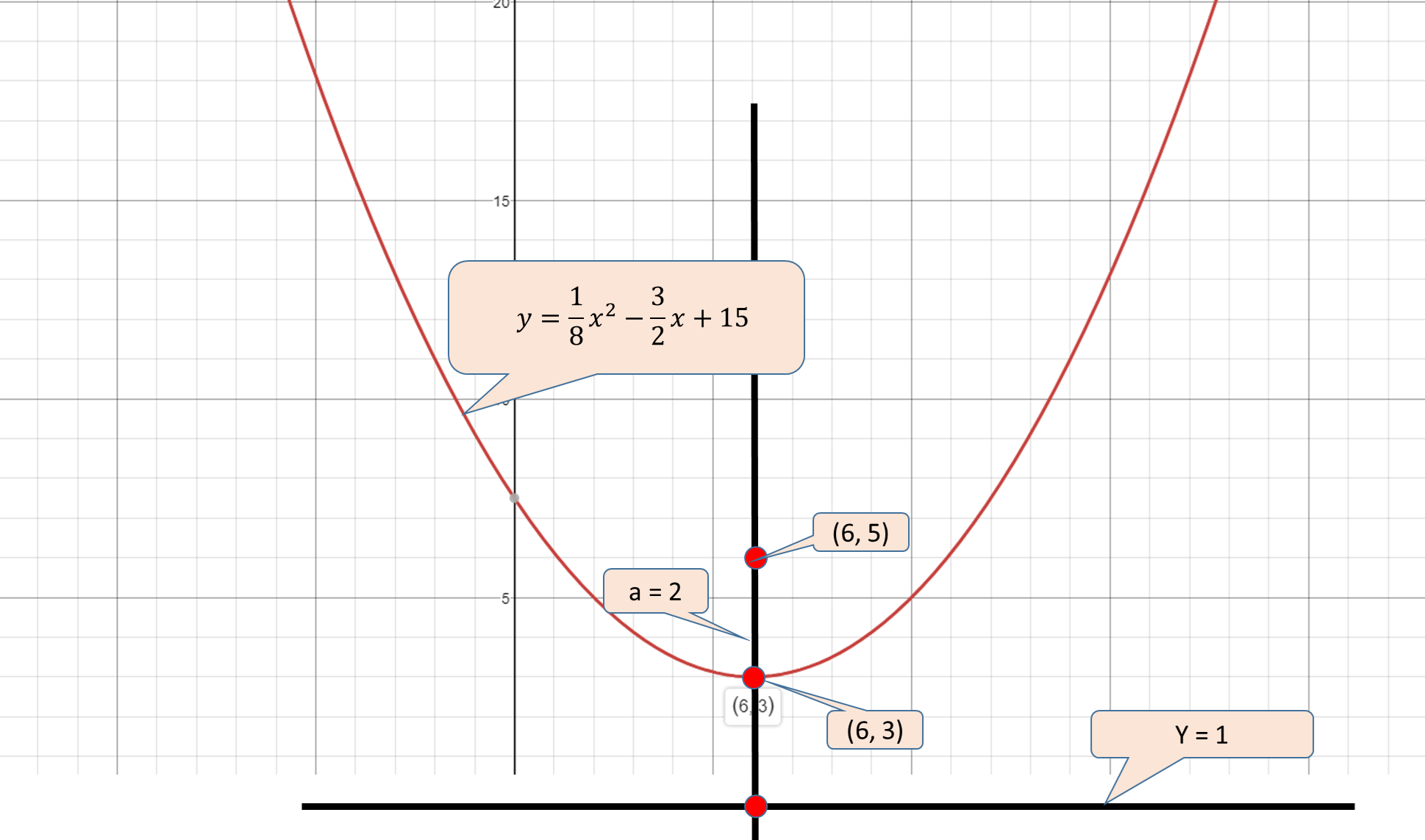
Look at the graph
The equation of the Parabola is -

#(x-h)^2=4a(y-k)#

Where -

#h=6# x coordinate of the vertex
#k=3# y coordinate of the vertex
#a=2# Distance between vertex and focus

Distance between Directix and vertex is the same as distance between vertex and focus

#(x-6)^2=4xx2xx(y-3)#
#x^2-12x+36=8y-24#
#8y-24=x^2-12x+36#
#8y=x^2-12x+36+24#
#8y=x^2-12x+60#
#y=1/8x^2-3/2x+15/2#