What is the standard form of #y=(2x+4)(x-5) #?

Question

2894 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-24T19:32:55

#y = 2x^2 - 6x - 20#

#y = (2x+4)(x-5)#

Standard quadratic form is #y = ax^2 + bx + c#.

Use FOIL to simplify:
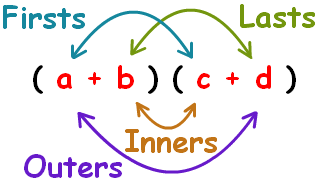
enter image source here

Following this image, we can simplify/expand:
Firsts:
#2x * x = 2x^2#

Outers:
#2x * -5 = -10x#

Inners:
#4 * x = 4x#

Lasts:
#4 * -5 = -20#

Combine them all together:
#y = 2x^2 - 10x + 4x - 20#

Combine the like terms #-10x# and #4x#:
#y = 2x^2 - 6x - 20#

As you can see, this is in standard quadratic form #y = ax^2 + bx + c#

Hope this helps!