What is the standard form of #y= (x+3) (x+4) #?
3 Answers
Explanation:
the standard form of a second-degree polynomial function should look like this
so we try to reach that for with your function
Using the Distributive property
Multiply
Add like terms
Explanation:
The standard form of a quadratic equation is
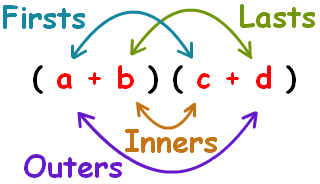
Following this image, we can multiply it out.
The
The
The
The
Combine them all together to get:
We can still combine the like terms
As you can see, this matches the form
Hope this helps!
Explanation:
#"the standard form of a quadratic is "#
#•color(white)(x)y=ax^2+bx+c color(white)(x);a!=0#
#"expanding the factors gives"#
#y=x^2+7x+12larrcolor(red)"in standard form"#


