3, -6, 12, -24, ...
You can rewrite this as:
(-1)^n 3*(1, 2, 4, 8, ...)
If we focus on 1, 2, 4, 8...
a_(n+1) = 2a_n
with a_0 = 1.
This can be written out as a nice sum:
sum_(n=0)^(N) 2^n = 2^0 + 2^1 + 2^2 + 2^3 + ...
= 1 + 2 + 4 + 8 + ...
Thus, now we can recombine everything to get:
color(green)(3sum_(n=0)^(N) (-1)^n 2^n)
where N is some arbitrary stop point.
The formula for summing this is:
 )
)
r = -2
(since (-1)^n * 2^n = (-2)^n)
a = 3
n = 10
=> 3((1-(-2)^10))/(1+2) -> (-2)^10 = 2^10
= 3((1-2^(5*2))/3)
= cancel(3)(1-32^2)/cancel(3) = 1-1024 = color(blue)(-1023)
To sum this up more easily than brute-forcing it, if you don't remember the formula, there's something rather creative you can do.
If you look at the odd-indexed terms (-6, -24, -96, -384, etc), you can see that they are all successively multiplied by 4. You can see that the even terms (3, 12, 48, 192, etc) are also this way. Thus, it lines up like so:
n = 0 " " " 2 " " " 4 " " " " 6:
" " 3 + 12 + 48 + 192 + ...
n = 1 " " " 3 " " " 5 " " " " 7:
-6 -24 -96 -384 - ...
and you always subtract twice the value of the positive number. Thus, just add up the first five even-indexed numbers (indices 0, 2, 4, ...) and switch the sign.
= -(3 + 12 + 48 + 192 + 768)
= -3(4^n)
with n_0 = 0
= -3(4^n) = -3[4^0 + 4^1 + 4^2 + 4^3 + 4^4 + 4^5]
= -3(1 + 4 + 16 + 64 + 256)
= -3(341) = color(blue)(-1023)
(You didn't have to write down as many terms here.)
Or, try adding up the original to check:
= 3 - 6 + 12 - 24 + 48 - 96 + 192 - 384 + 768 - 1536)
= -3 - 12 - 48 - 192 - 768
= -15 - 240 - 768
= -255 - 768
= -223 - 800 = color(blue)(-1023)
(Except now you had to write out 10 terms to add up.)
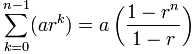 )
) 
