Question

What is the surface area to volume ratio for a cube that measures 4 cm on each side?

Answer 1

`A = 96 cm^2`
`V = 64 cm^3`
`Ratio =(96cm^2)/(64cm^3) = 1.5`

Explanation:

You calculate the total surface area by finding the area of a single side of the cube and then multiplying that area by six (for the six sides of a cube).

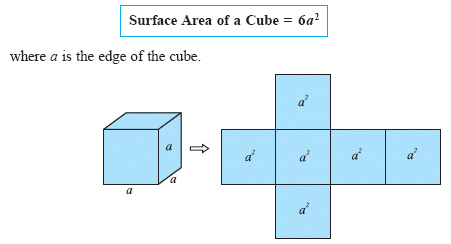
Once you do this you will find that a 4cm Cube has a total surface area of `96cm^2`.

To find the volume you simply use the following formula:

`V_(cube)=L*W*H`

In this case (because it is a cube) you will use 4cm for each value:

`V_(cube) = 4cm*4cm*4cm=64cm^3`

To find the ratio of surface area to volume, simply divide the surface area by the volume:

Ratio `=(96cm^2)/(64cm^3)=1.5`

Ratios are generally unit-less as they are comparing two values rather than combining to form a new value.