Question

What is the symmetric difference of sets A and B?

`A=[1,4,9,10,15] and B=[2,4,7,10]`

Thanks

Answer 1

See below.

Explanation:

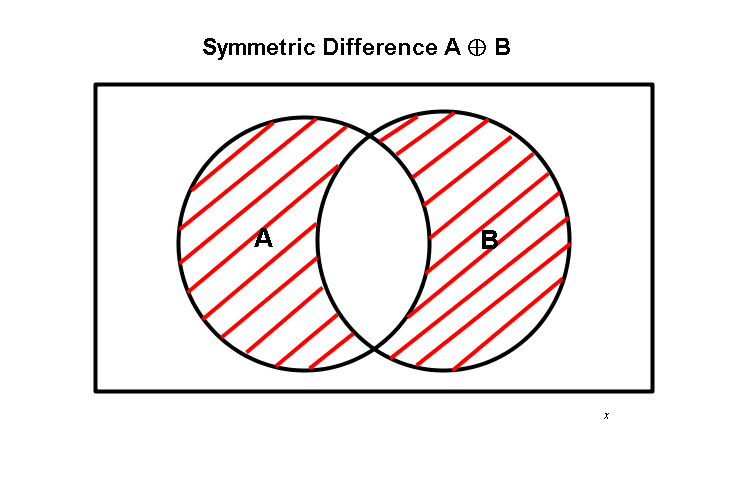
The symmetric difference of two sets A and B, is the set that contains the elements of A and the elements of B, but not the elements of their intersection.

The notation used to represent this can vary, between:

`o+` , `⊝` or `Delta`

Our sets are:

`A={1,4,9,10,15}`

`B={2,4,7,10}`

The intersection is:

`AnnB={4,10}`

We can view this as subtracting `AnnB` from `AuuB`

`AuuB color(white)(8)\\\AnnB=Ao+B={1,2,7,9,15}`

Note the use of `\\\\`.

This is really saying that the symmetric difference of A and B is the relative compliment of their intersection. i.e. everything in `AuuB`. that is not in `AnnB`

The Venn diagram below shows the symmetric difference as the shaded area:

The reasoning of the relative compliment can be found here

https://socratic.org/questions/what-is-the-complement-of-b-relative-to-a-for-sets-a-1-5-8-10-12-and-b-2-4-5-8-1#538631