Question

What is the total force on any arbitrary current carrying wire in a uniform magnetic field ?

Answer 1

`F=BILsintheta`

Explanation:

The force on the wire is proportional to:

Current `I`

Length of wire in the field `L`

Sine of angle conductor makes with field `sintheta`

The magnetic flux density `B`

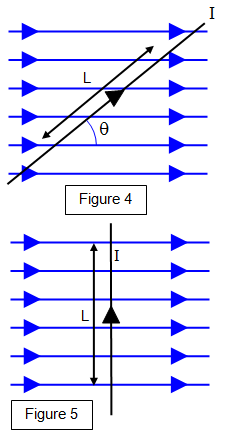
Figure 4 shows a wire at an angle `theta`. The perpendicular vector of the magnetic field that the wire experiences will be equal to `cos(90-theta)` = `sintheta`.

The force on the wire is given by:

`F=BILsintheta`

From figure 5 you can see that if the wire is perpendicular to the field then `theta=90` and `sintheta=1`.

In this case the force is at a maximum where:

`F=BILsin90`

`=BIL`

In terms of vectors:

`F=BIstackrel(rarr)(L)`

`stackrel(rarr)(L)` is the vector from the start point to the end point. In the case of a closed loop, the wire starts and ends at the same place so:

`stackrel(rarr)(L)=0`

So:

`F=BIxx0=0`