Start by factoring the numerator:
#= lim_(x->2) (((x + 3)(x-2))/(x-2))#
We can see that the #(x - 2)# term will cancel off. Therefore, this limit is equivalent to:
#= lim_(x->2) (x + 3)#
It should now be easy to see what the limit evaluates to:
#= 5#
Let's take a look at a graph of what this function would look like, to see if our answer agrees:
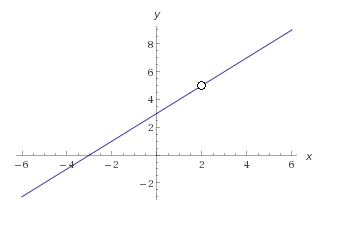
The "hole" at #x = 2# is due to the #(x - 2)# term in the denominator. When #x = 2#, this term becomes #0#, and a division by zero occurs, resulting in the function being undefined at #x = 2#. However, the function is well-defined everywhere else, even when it gets extremely close to #x = 2#.
And, when #x# gets extremely close to #2#, #y# gets extremely close to #5#. This verifies what we demonstrated algebraically.


