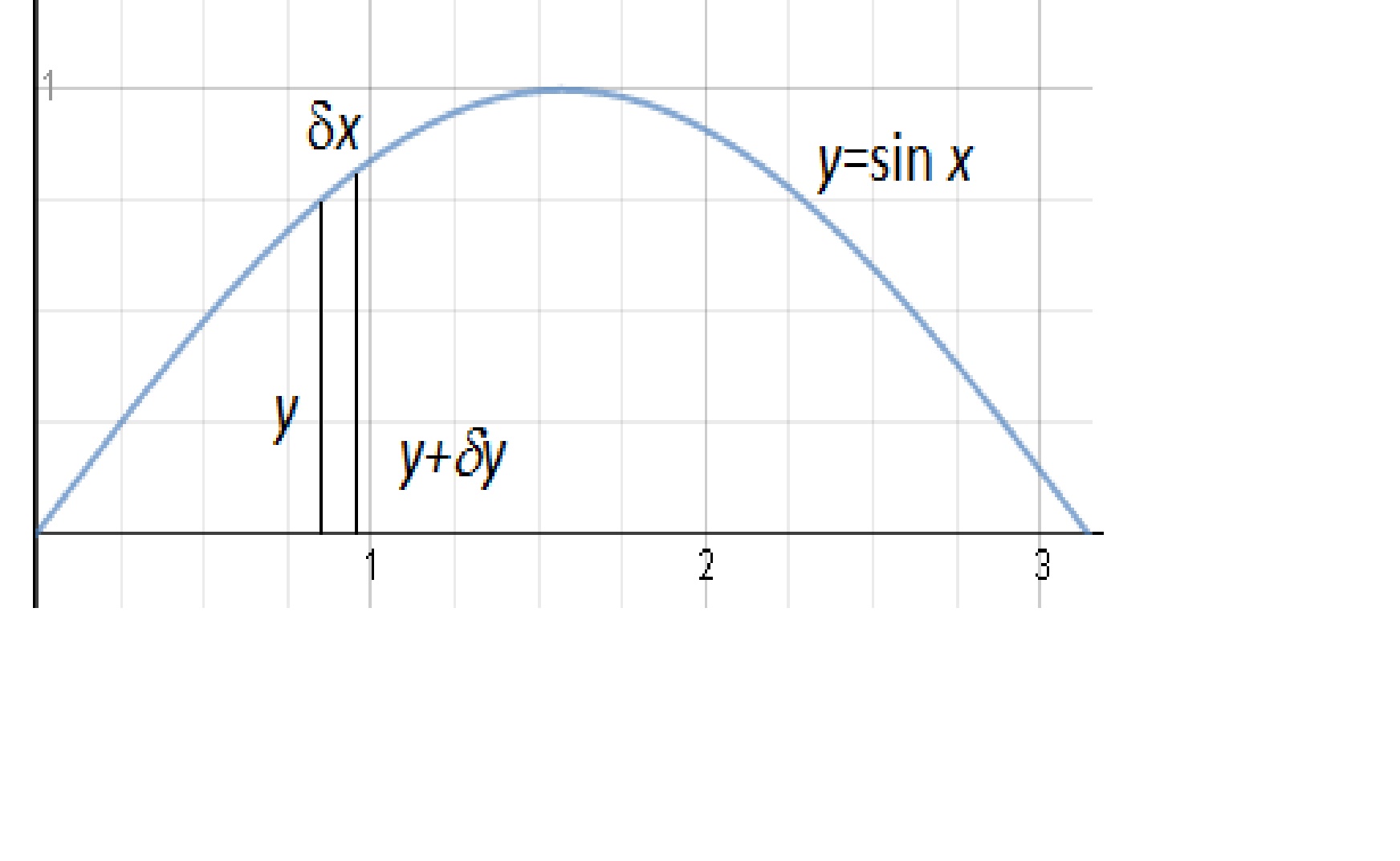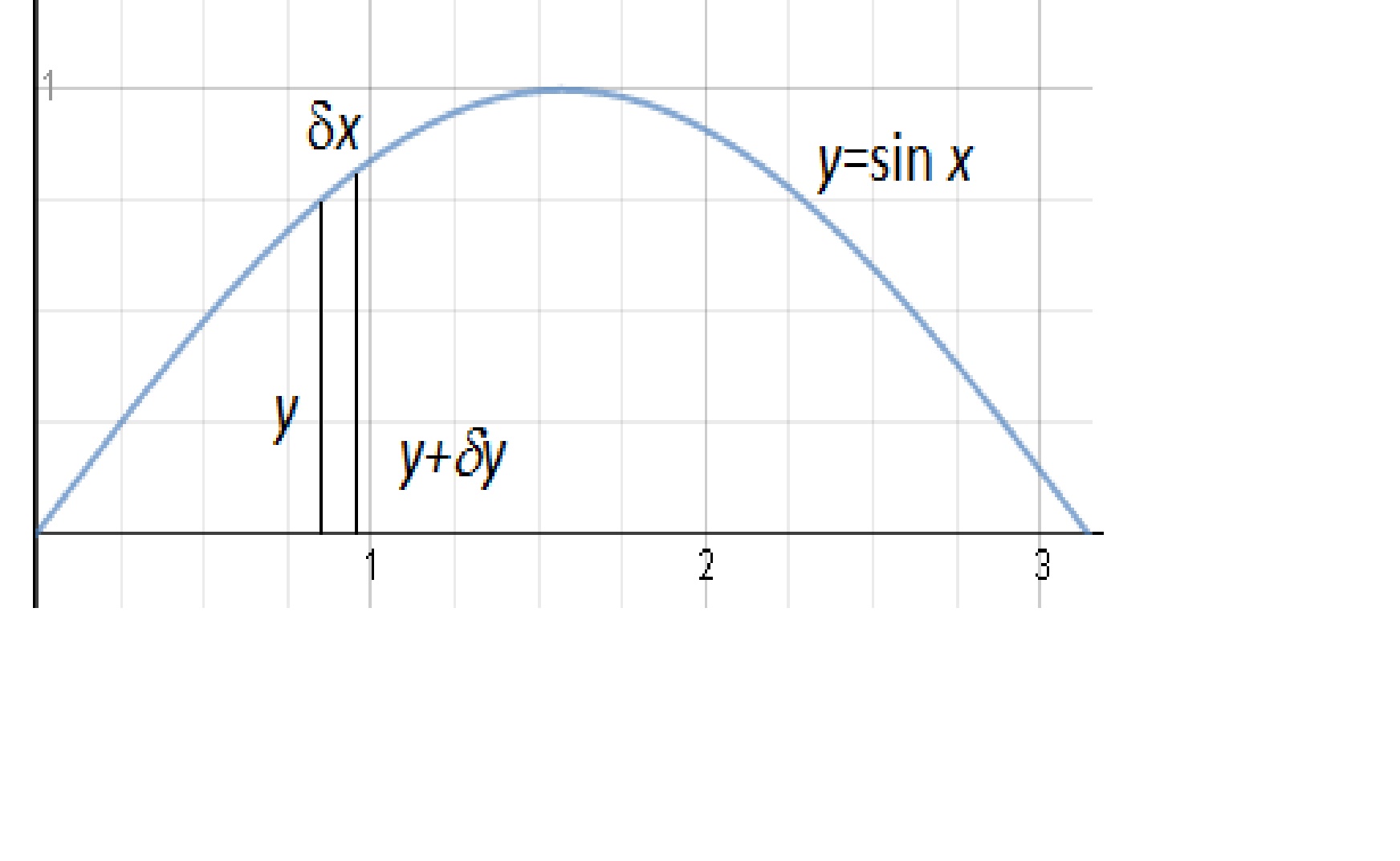
We have drawn the given expression #f(x)=sinx#, for #x=0# to #x=pi#. When this expression is revolved around #x# axis through #360^@# we have solids of revolution. At each point located on the graph, the cross-section of the solid, parallel to the #y#-axis, will be a circle of radius #y#.
Let us consider a thin disc of thickness #deltax#, at a distance #x# from the origin, with its face nearest to the #y#-axis. The radius of the other circular face of the disc will be #y+δy#.
The disc is not a perfect cylinder. It will become one when #δx#, and hence #δy->0#.
Thus we approximate the disc with a cylinder of thickness, #δx# and radius #y#.
The volume #δV# of the disc is then given by the volume of a cylinder, #πr^2h#, so that
#δV=πy^2δx#.
We have ignored the volume of part of the disc which is #prop(deltax xx delta y)#, both being infinitesimally small.
So the volume #V# of the solid of revolution is given by the integral of volume expression over the limits of interest as both #δx->0# and #δy->0#.
#V=int_a^b πy^2dx#
Inserting values given in the problem we obtain
#V=int_0^pi π(sinx)^2.dx#
or #V=int_0^pi πsin^2x.dx# .....(1)
-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.
To find the #intsin^2x.dx#
From trigonometric identity #sin^2x=1/2(1-cos2x)#
#:.# we need to find #int1/2(1-cos2x).dx#
#=>int1/2dx-1/2intcos2x.dx#
Integrating first term and for the second term
let #u=2x#. Differentiating both sides and inserting in the equation
#du=2dx#
#=>x/2-1/4intcosu. du#
#=>x/2-1/4intcosu.du#
#=>x/2-1/4 sin u#, substituting back to #x#
#=>x/2-1/4sin 2x#
We have ignored the constant of integration as we are eventually dealing with definite integral.
-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-.-
Substituting the value of integral in (1)
#V=pi[x/2-1/4sin 2x]_0^pi#
#V=pi[(pi/2-1/4sin 2pi)-(0/2-1/4sin (2xx0))]#, inserting the value of #sin2pi and sin 0, "both" =0#
#V=pi^2/2#