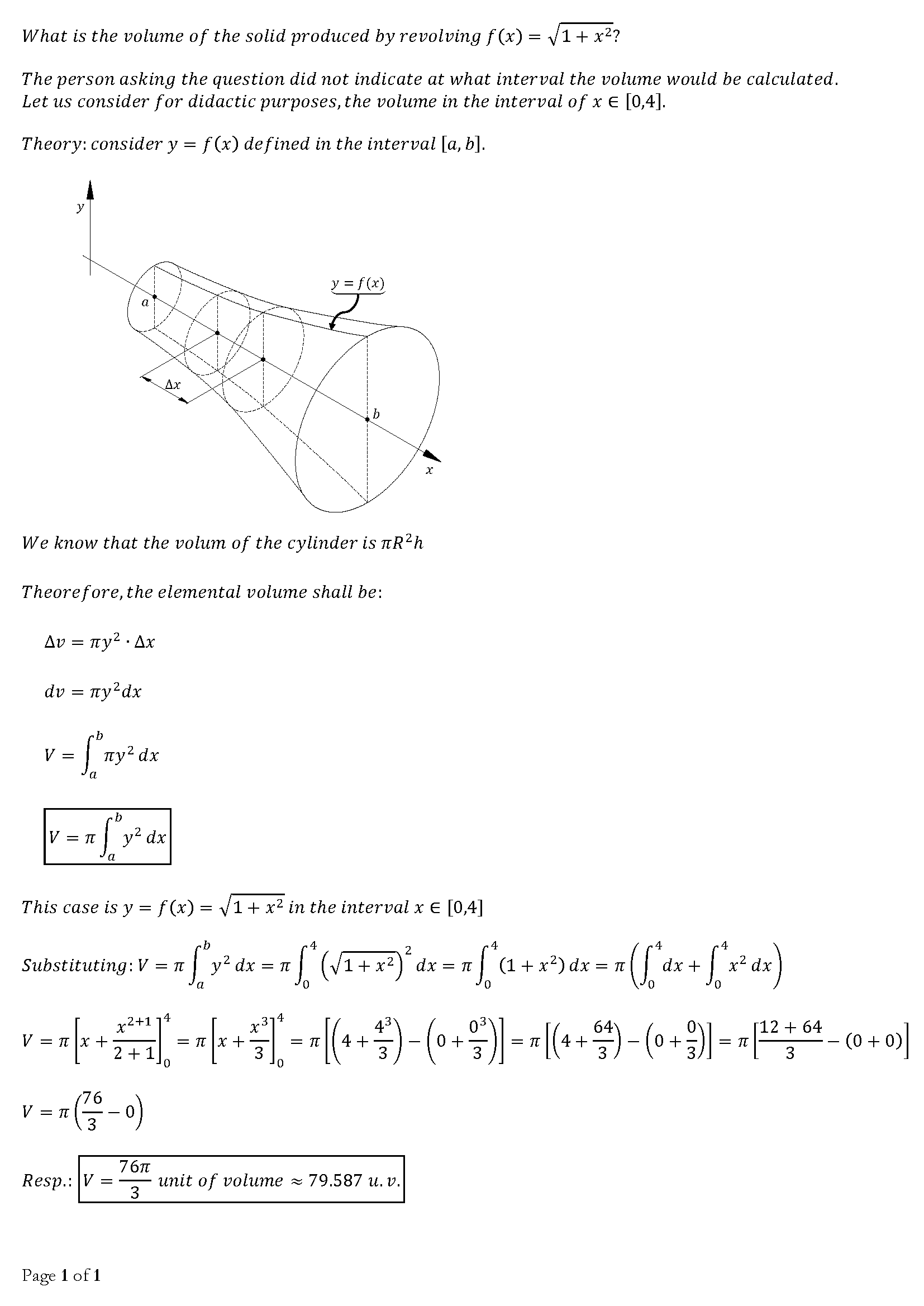What is the volume of the solid produced by revolving #f(x)=sqrt(1+x^2)# around the x-axis?
2 Answers
Nov 17, 2016
# V = pi[x+1/3x^3]_a^b #
Explanation:
The volume of revolution about
# V = int_a^b piy^2dx #
so with
# V = int_a^b pi(sqrt(1+x^2))^2dx #
# :. V = piint_a^b 1+x^2 dx #
# :. V = pi[x+1/3x^3]_a^b #
As you have not specified the
Nov 17, 2016
See answer below: