Question

What is the volume of the solid produced by revolving `f(x)=sqrt(81-x^2)` around the x-axis?

Answer 1

Volume `color(blue)(V=972 pi" ")`cubic units

Explanation:

Solution 1.

The given curve is located at the first and second quadrants as shown in the graph

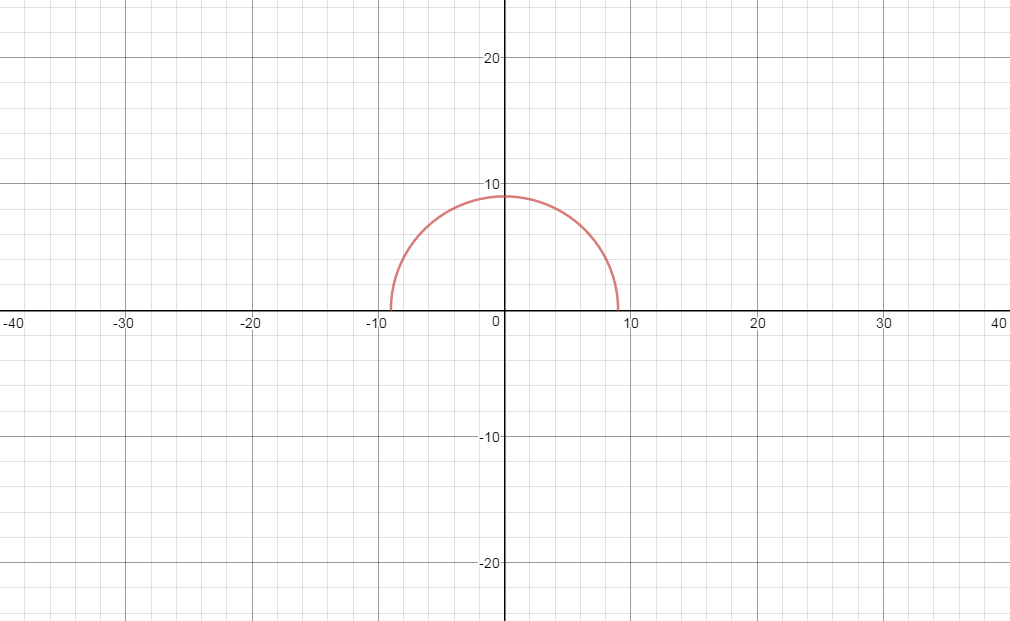
You will notice that the graph shows that it is a half circle with radius `r=9" "`units. If we revolve this about the x-axis the solid form is a sphere.

Formula for volume of the sphere

`V=4/3 pi r^3`

`V=4/3 pi 9^3`

`V=4/3 pi 729`

`color(blue)(V=972 pi" ")`cubic units

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Solution 2.

To solve for the volume by the Calculus , we make use of the Disk Method

`dV=pi r^2 dh`

`dV=pi y^2 dx`

`V=int_(-9)^9 pi*y^2 dx=pi*int_(-9)^9 sqrt((81-x^2))^2 dx`

`V=pi*int_(-9)^9 (81-x^2) dx`

`V=pi*[81x-x^3/3]_(-9)^9`

`V=pi*[81*9-9^3/3-(81(-9)-(-9)^3/3)]`

`V=pi*[729-729/3-(-729+729/3)]`

`V=pi*[729-243+729-243]`

`color(blue)(V=972 pi" ")`cubic units.

God bless....I hope the explanation is useful.