What is the volume of the solid produced by revolving #f(x)=x^2-x+1, x in [1,3] #around #x=1#?
2 Answers
Explanation:
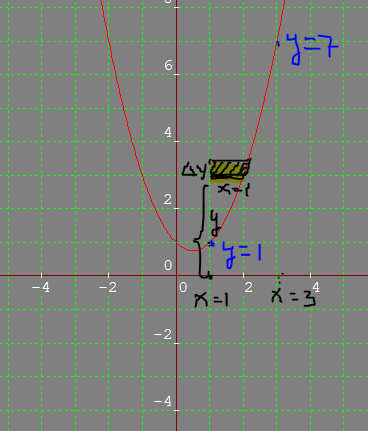
The given function is a parabola opening upwards, as shown in the figure. The portion to revolved lies between x=1 and 3 and the axis of revolution is x=1
Now consider an elementary strip of thickness
The volume of the whole solid so generated would be
From the given eq y=
=
=
=
=
=
The region is not fully specified. I'll answer both possible questions.
Explanation:
Upper Region
If the region is above the parabola and below
The region bounded by the functions is shown below in red.
If we take a representative slice parallel to the axis of revolution we have a slice at
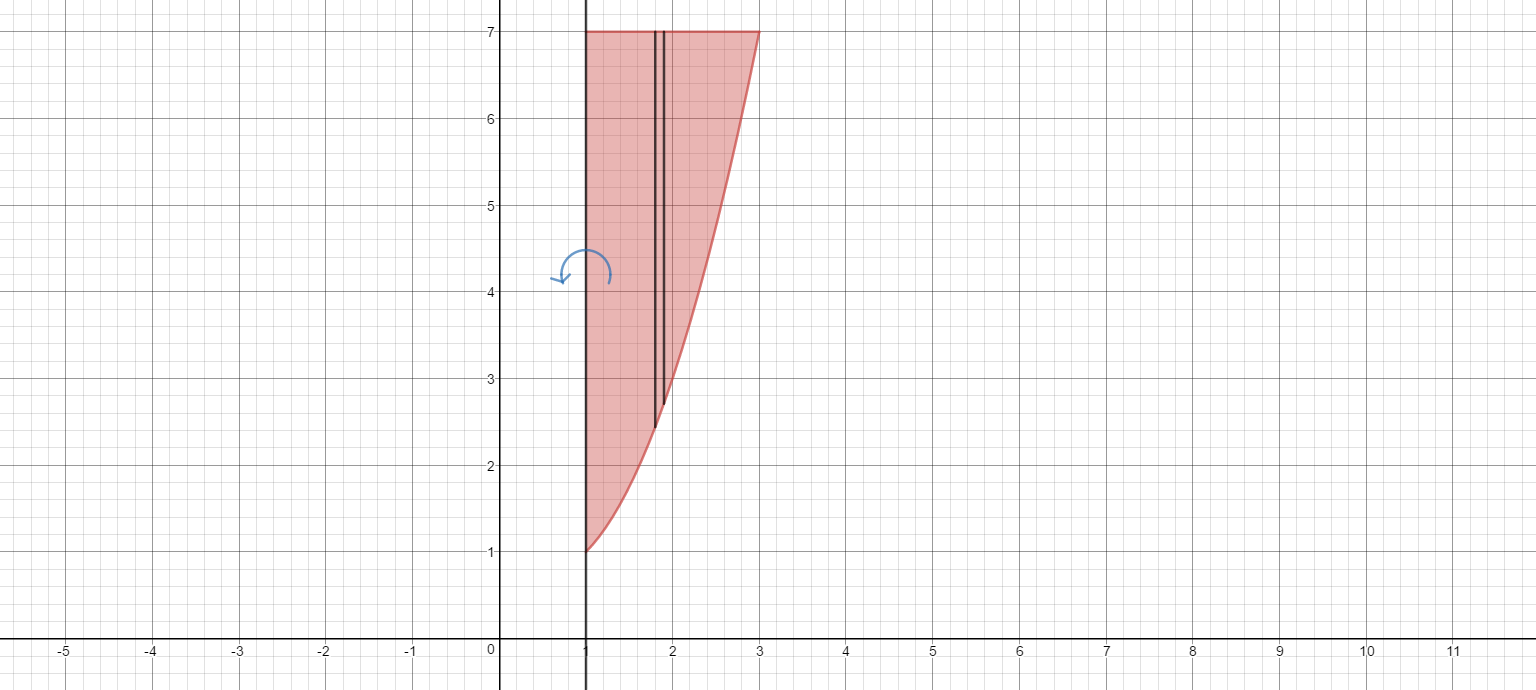
When we revolve the slice, we get a cylindrical shell with volume
In this case
(Because we're revolving around
and
(The height of the slice is the upper
The thickness is
The volume of the representative shell is:
We will be integrating with respect to
The volume of the solid is
# = 2pi int_1^3 (x-1)(7-(x^2-x+1))dx#
# = 2pi(16/3) = (32pi)/3#
LowerRegion
If the region is belowthe parabola and above the
The region bounded by the functions is shown below in red.
If we take a representative slice parallel to the axis of revolution we have a slice at
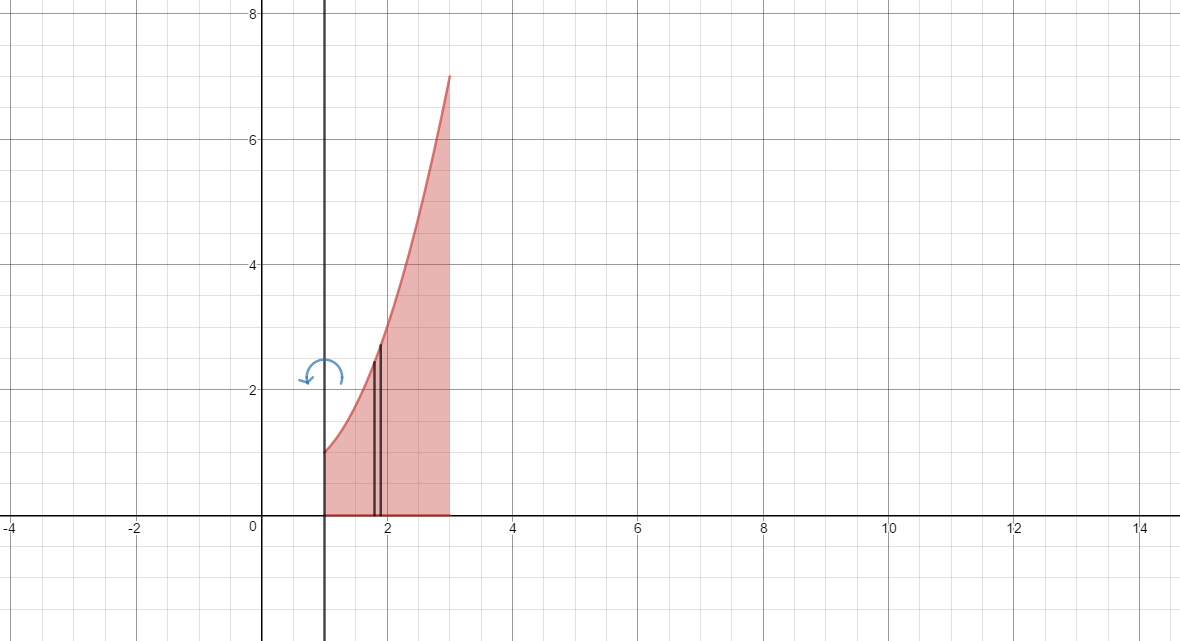
When we revolve the slice, we get a cylindrical shell with volume
In this case
(Because we're revolving around
and
(The height of the slice is the upper
The thickness is
The volume of the representative shell is:
We will be integrating with respect to
The volume of the solid is
# = 2pi int_1^3 (x-1)(x^2-x+1)dx#
# = 2pi(26/3) = (52pi)/3#

