Question

What is the volume of the solid produced by revolving `f(x)=x^3-2x+3, x in [0,1]`around the x-axis?

Answer 1

Here's a TI screenshot of the answer:

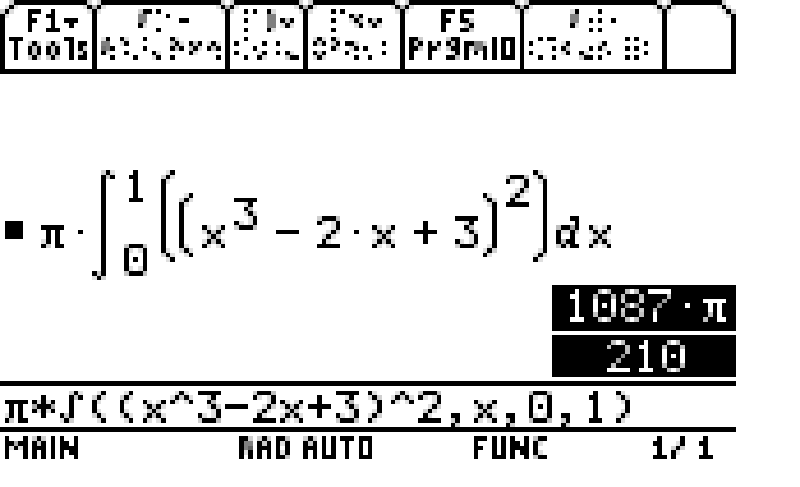
As a decimal expansion, we have :

Explanation:

When you integrate area, you get volume. In other words, if you go backwards from area, you'll get volume.

So you just integrate with the standard disc method :

`pi* int r^2dx`.

Here, `pi*r^2` represents the area of a circle. It becomes a disc when you multiply this expression by the height dx (this product yields a 3- dimensional object) . It's like a bunch of quarters of varying radii.

Here, `r = x^3-2x+3`

That's the actual radius of your disc., varying as a function of x.

Here is a pretty pic:

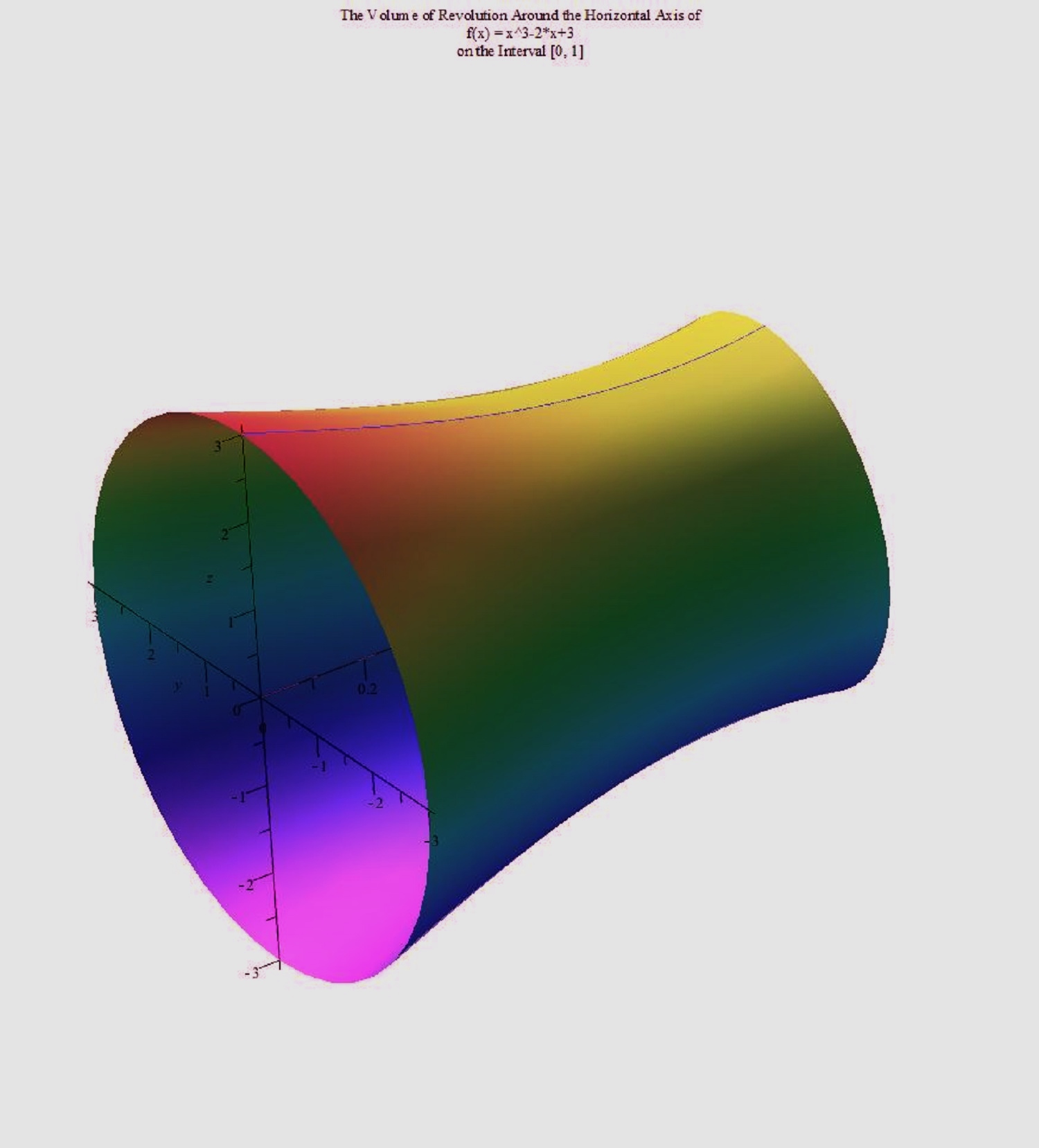
I did this in Maple...and yes, Maple freakin' rules.

Finally, you need to "get your hands dirty" and fill in all the algebraic details as far as arriving at the antiderivative and then crunching the bounded definite integral.

That's your job.