What is the volume of water in a trough when the depth of the water is d?
A water trough is 6 m long and its cross-section is an isosceles trapezoid which is 100 cm wide at the bottom and 200 cm wide at the top, and the height is 50 cm. The trough is not full. Give an expression for V, the volume of water in the trough in #cm^3# , when the depth of the water is d cm.
A water trough is 6 m long and its cross-section is an isosceles trapezoid which is 100 cm wide at the bottom and 200 cm wide at the top, and the height is 50 cm. The trough is not full. Give an expression for V, the volume of water in the trough in
2 Answers
Explanation:
#"refer to Sean's solution"#
Explanation:
.
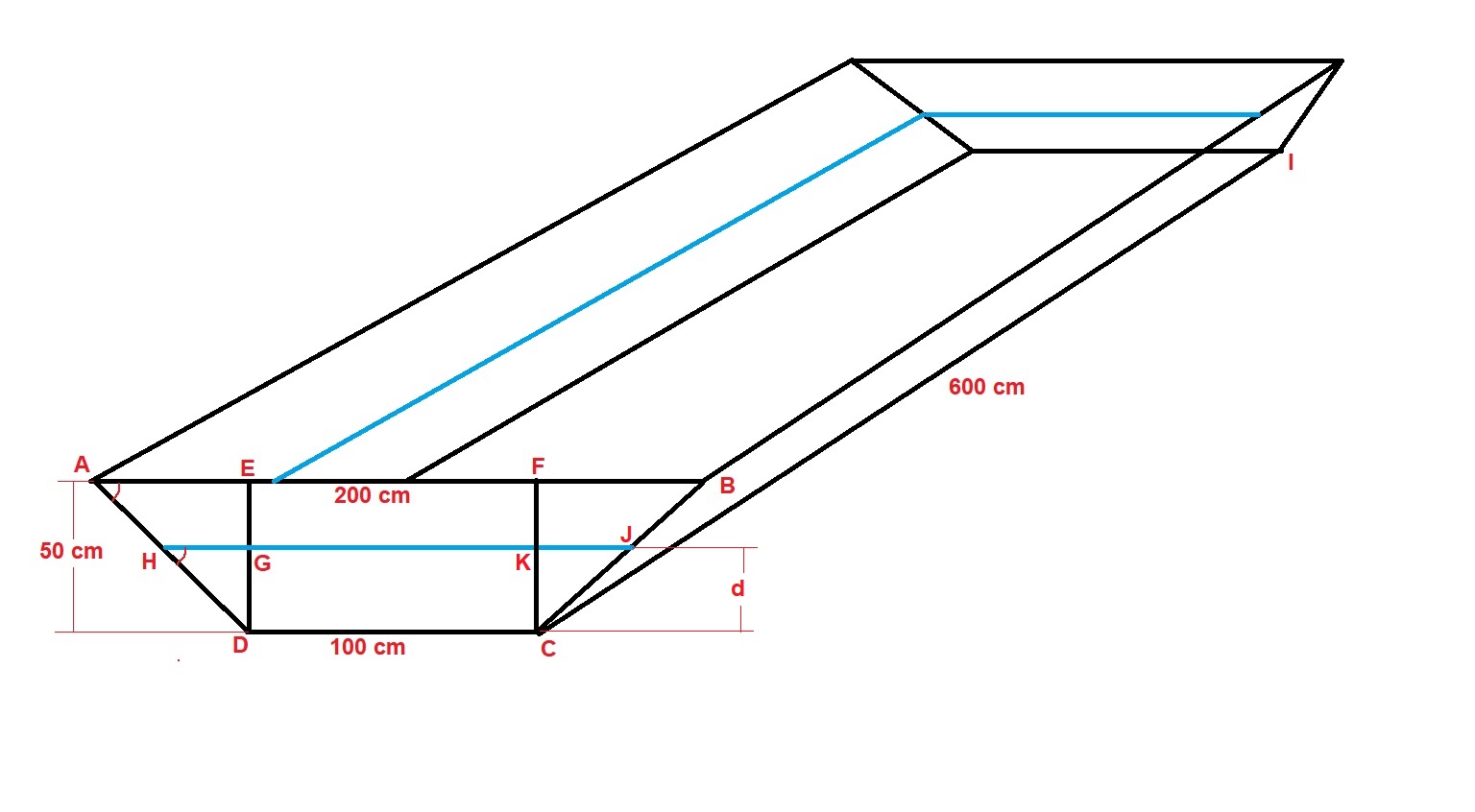
The figure above shows the trough described in the problem. The front and back of the trough are isosceles trapezoids. The trough itself is a trapezoidal prism. The volume of prism is calculated by multiplying the area of the trapezoid
But we are asked to figure out the volume of the water in the trough, and the trough is not full.
The water level in the trough is shown by blue lines. The water in the trough forms a smaller trapezoidal prism whose length is the same as the length of the trough.
But the trapezoids in the front and the back of the water prism are smaller than those of the trough itself because the depth of the water
As the water level varies in the trough,
The volume of water is calculated by multiplying the area of trapezoid
Since we have to find an expression for
The large base is
Since trapezoid
For the same reason:
THe right triangle
Triangle
Therefore,
Area of a trapezoid
Area of trapezoid

