What is the wavelength, in nm, of a photon emitted during a transition from the n = 5 state to the n = 2 state in the hydrogen atom ?
2 Answers
This should be a transition in the so called "Balmer Series":
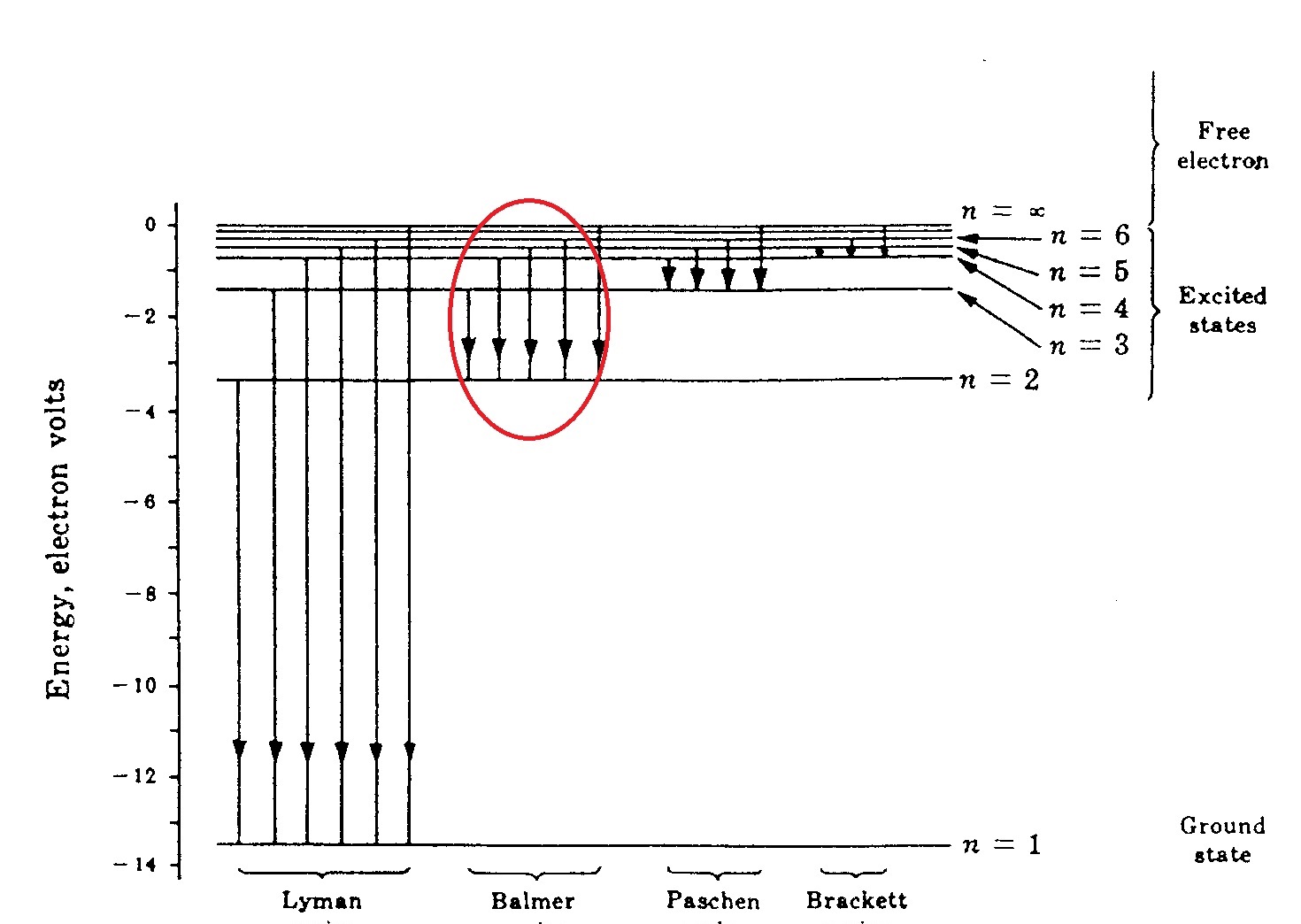
(Picture from Ohanian Physics)
You can use the fact that a photon emitted during the transition from n = 5 to n = 2 will carry an energy
Knowing this, you can relate the energy of the photon with the frequency
#E=hnu# (
#h# is Planck's constant.)
For any state corresponding to
#E_n= -"13.6 eV"/n^2# ,where
#-"13.6 eV"# is the approximate ground-state energy of the hydrogen atom.
So:
#E_2 = -"13.6 eV"/4 = -"3.4 eV" = -5.44*10^-19# #"J"#
#E_5 = -"13.6 eV"/25 = "0.544 eV" = -8.7*10^-20# #"J"#
So,
#DeltaE = 4.57*10^-19# #"J"# .
In
#nu=(4.57*10^-19 "J")/(6.63*10^-34 "J" cdot"s") = 6.892*10^14 "s"^(-1)# ,but
#c=lambdanu# (#c# is the speed of light);
So,
#lambda=(3*10^8 "m/s")/(6.892*10^14 "s"^(-1)) xx (10^9 "nm")/("1 m") = ul"435 nm"#
Explanation:
Since,
Putting in the values of physical constants
Here,



