What is the wavelength of a photon of blue light whose frequency is #6.3 * 10^14# #s^-1#?
1 Answer
Explanation:
The key to any frequency and wavelength problem is the fact that frequency and wavelength have an inverse relationship described by the equation
#color(blue)( lamda * nu = c)" "# , where
So, what does an inverse relationship mean?
In simple words, that equation tells you that when frequency increases, wavelength must decrease in order for their product to remain constant.
Likewise, when frequency decreases, wavelength must increase in order for their product to remain constant.
As a consequence of this, you can expect waves that have short wavelengths to also have high frequencies, and waves that have long wavelengths to also have short frequencies.
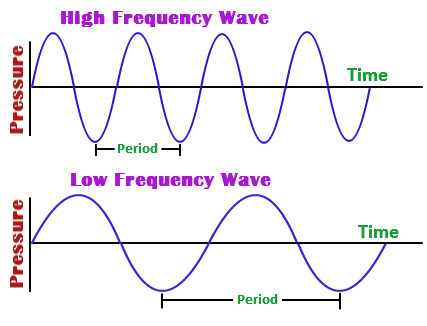
In your case, the wave has a relatively high frequency, so you can predict a relatively short wavelength.
Another important thing to notice in such problems is the fact that the units used to express the frequency match those used to express the speed of light.
This tells you that you don't have to do any unit conversions.
So, plug in your values to get
#lamda * nu = c implies lamda = c/(nu)#
#lamda = (3 * 10^8 "m" color(red)(cancel(color(black)("s"^(-1)))))/(6.3 * 10^14 color(red)(cancel(color(black)("s"^(-1))))) = color(green)(4.8 * 10^(-7)"m"#
The answer is rounded to two sig figs. You can express this wavelength in nanometers by using the conversion factor
#"1 m" = 10^9"nm"#
This will give you
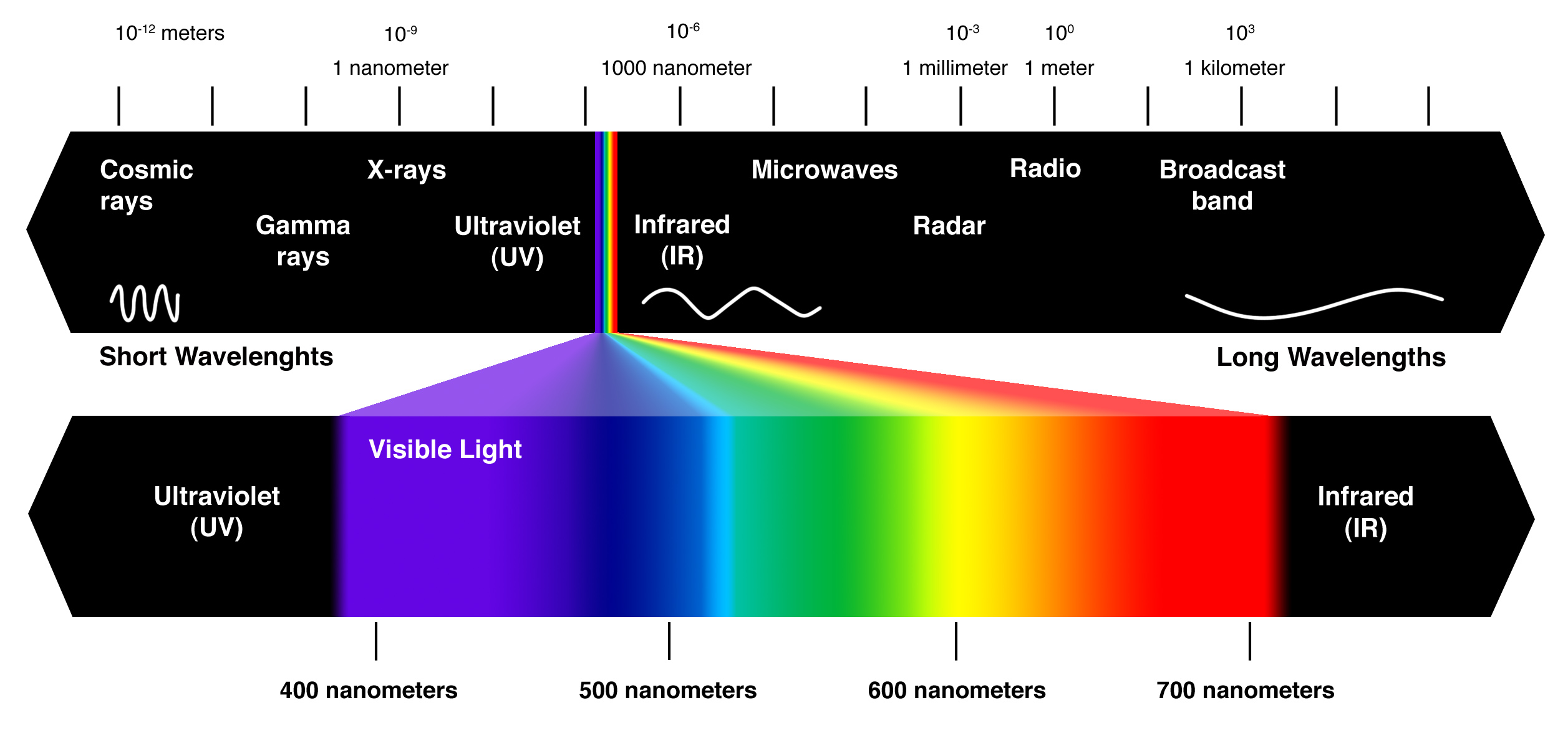
This wavelength places your wave in the visible part of the electromagnetic spectrum. More specifically, this wave would be located in the blue region of the spectrum.