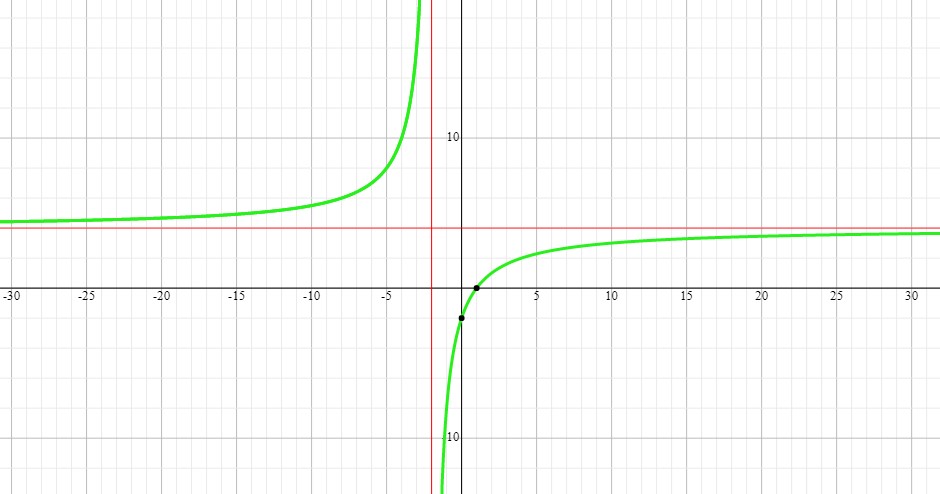
What is the y-intercept, vertical and horizontal asymptote, domain and range?
#
(4x − 4)/(x + 2)
#
1 Answer
Please see below.
Explanation:
.
We can find the
Vertical asymptote can be found by setting the denominator equal to
Horizontal asymptote can be found by evaluating
To find the limit, we divide both the numerator and denominator by the highest power of
As you see,
If you have not been taught how to find limits of functions yet you can use the following rules:
1) If the degree of the numerator is the same as the degree of the denominator the horizontal asymptote is
2) If the degree of the numerator is smaller than the degree of the denominator the horizontal asymptote is
3) If the degree of the numerator is larger than the degree of the denominator you do not have a horizontal asymptote rather you have a slant asymptote in addition to any vertical one(s).
Domain of the function is defined in two pieces because we have one vertical asymptote which means the function is not continuous and has two parts - one on each side of the vertical asymptote:)#
Domain:
This shows that
The same goes for Range. As you can see this rational function has each of its two pieces on one side of the horizontal asymptote.
Range: