What mass of benzoic acid, #C_6H_5COOH#, would you dissolve in 400.0 mL of water to produce a solution with a pH = 2.95?
Equation:
#C_6H_5COOH+H_2O⇌H_3O^++C_6H_5COO^-#
#Ka=6.3×10^(-5)#
Website response:
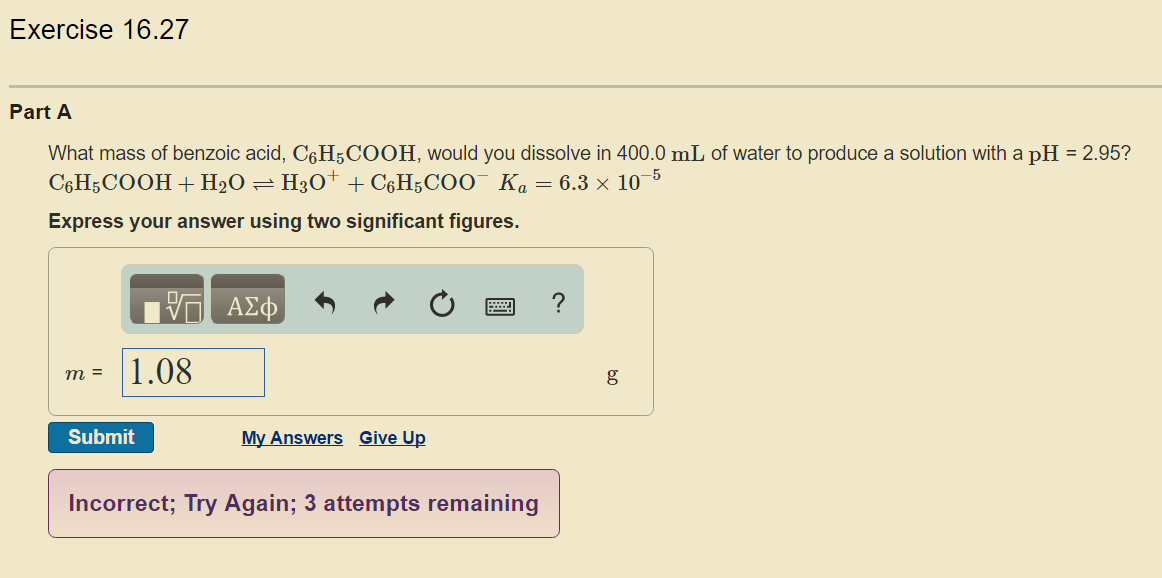
My work
So far, I haven't found any issues...
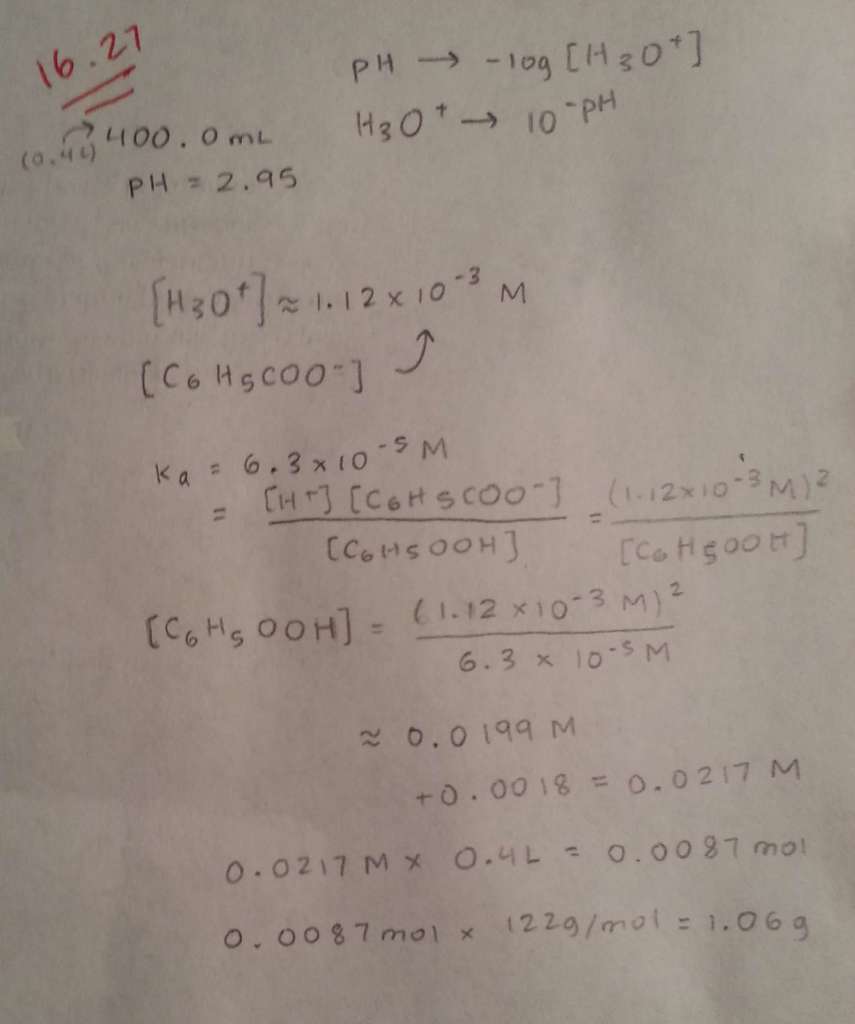
Equation:
Website response:
My work
So far, I haven't found any issues...
1 Answer
Here's what I got.
Explanation:
I'll just solve this problem from scratch so that you can follow my reasoning and see where you made the error.
So, you know that
#"C"_ 6"H"_ 5"COOH"_ ((aq)) + "H"_ 2"O"_ ((l)) rightleftharpoons "C"_ 6"H"_ 5"COO"_ ((aq))^(-) + "H"_ 3"O"_ ((aq))^(+)#
The acid dissociation constant for benzoic acid is defined as
#K_a = (["H"_3"O"^(+)] * ["C"_ 6"H"_5"COO"^(-)])/(["C"_6"H"_5"COOH"])#
Now, you know that
#["H"_3"O"^(+)] = 10^(-2.95)#
#["H"_3"O"^(+)] = 1.12 * 10^(-3)"M"#
As you can see from the ionization equilibrium, every mole of benzoic acid that ionizes produces
This means that at equilibrium, you will have
#["H"_3"O"^(+)] = ["C"_6"H"_5"COO"^(-)]#
Consequently, you can say that
#["C"_6"H"_5"COO"^(-)] = 1.12 * 10^(-3)"M"#
Rearrange the equation you have for
#["C"_6"H"_5"COOH"] = (["H"_3"O"^(+)] * ["C"_6"H"_5"COO"^(-)])/K_a#
Plug in your values to find
#["C"_6"H"_5"COOH"] = (1.12 * 10^(-3))^2/(6.3 * 10^(-5)) = 1.99 * 10^(-2)"M"#
Now, you know that this is how much benzoic acid remains in solution after
This means that the initial concentration of the acid was
#["C"_6"H"_5"COOH"]_0 = overbrace(1.99 * 10^(-2)"M")^(color(blue)("what remains unionized")) + overbrace(1.12 * 10^(-3)"M")^(color(purple)("what ionizes"))#
#["C"_6"H"_5"COOH"]_0 = 2.10 * 10^(-2)"M"#
You can assume that the volume of the solution is equal to that of water
#400.0 color(red)(cancel(color(black)("mL"))) * "1 L"/(10^3color(red)(cancel(color(black)("mL")))) = "0.400 L"#
which means that this solution will contain
#0.400 color(red)(cancel(color(black)("L"))) * (2.10 * 10^(-2)color(white)(.)"moles C"_6"H"_5"COOH")/(1color(red)(cancel(color(black)("L solution"))))#
# = 8.40 * 10^(-3)color(white)(.)"moles C"_6"H"_5"COOH"#
To find the mass of benzoic acid that will contain this number of moles, use the compound's molar mass
#8.40 * 10^(-3)color(red)(cancel(color(black)("moles C"_6"H"_5"COOH"))) * "122.12 g"/(1color(red)(cancel(color(black)("mole C"_6"H"_5"COOH")))) = color(darkgreen)(ul(color(black)("1.0 g")))#
The answer is rounded to two sig figs.
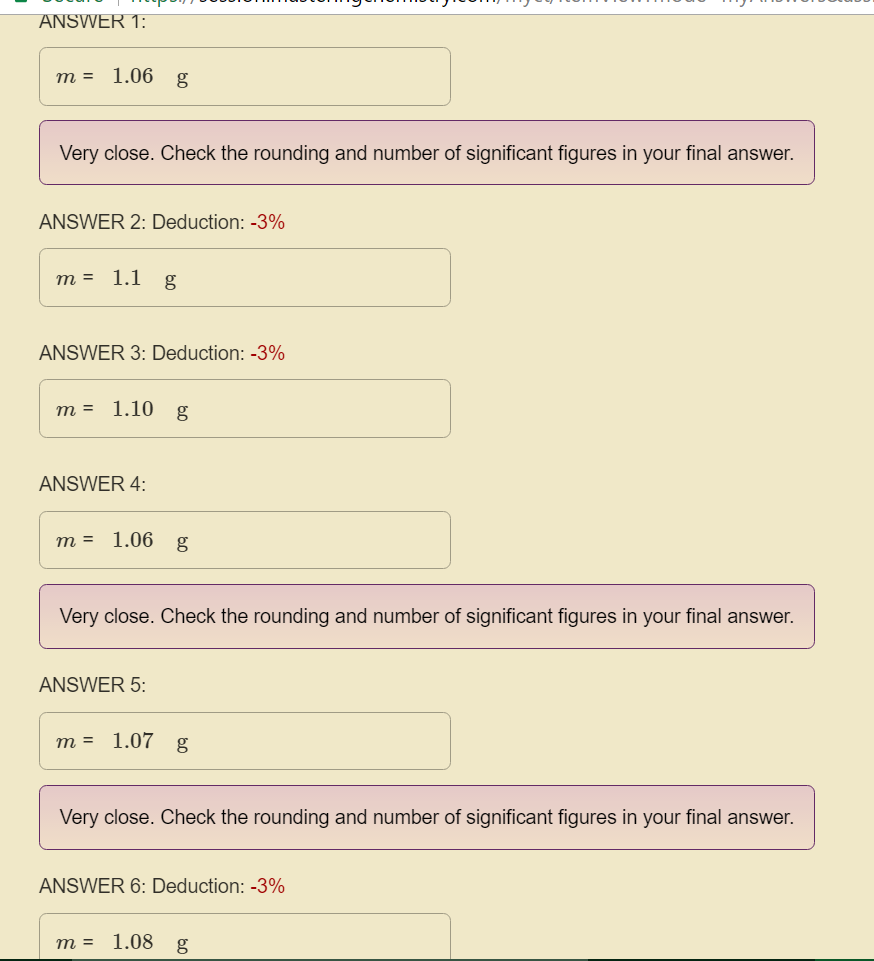
As a final note, it's worth pointing out that only one of your proposed solutions was rounded to two significant figures, the others were rounded to three sig figs!
#1.08, 1.10, 1.06, 1.07 -># three sig figs
Moreover, I'm not sure where
#"0.0199 M " + " 0.0018 M"#
came from. The concentration of the hydronium cations was actually

