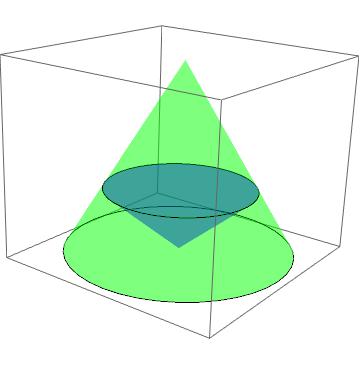
What must be the altitude of the inscribed cone in order to have the largest possible volume?

Question

A right circular cone is to be inscribed in another right circular cone of volume #3m^3# and altitude #2m# , with the same axis and with the vertex of the inner cone touching the base of the outer cone.

*** I would like to do it by myself first. But I'm just thinking if these 2 cone are similar in this case.

1419 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-11-20T19:43:01

#h = 2/3# [m]

Considering the external cone as

#C(R,H,V)#

and the internal cone as

#C(r,h,v)# we have

#R/H = r/(H-h) rArr r = (R/H)(H-h)#

now speaking in volumes

#v = 1/3 pi r^2 h = 1/3 pi (R/H)^2(H-h)^2 h#

and now

#(dv)/(dh) = 0 rArr H^2-4Hh+3h^2=0#

and solving for #h# we get

#h = {(H),(1/3H):}#

the first value corresponds to a minimum (#v = 0#) and the second value corresponds to a maximum (#v = 1/3pi R^2H xx 4/27 = 4/27 V#)

This for #h = H/3 =2/3# [m]

enter image source here